
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: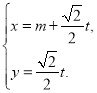 (
(![]() 是参数).以原点
是参数).以原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,曲线
为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,试求实数
,试求实数![]() 值;
值;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() 分别为线段
分别为线段![]() 的中点,在五棱锥
的中点,在五棱锥![]() 中,
中,![]() 为棱
为棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 分别交于点
分别交于点![]() .
.
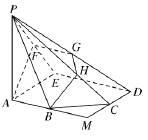
(1)求证:![]() ;
;
(2)若![]() 底面
底面![]() ,且
,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
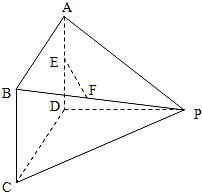
【题目】如图,四棱锥P﹣ABCD中,四边形ABCD是边长为2的正方形,△PAD为等边三角形,E,F分别为PC和BD的中点,且EF⊥CD.
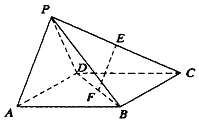
(1)证明:平面PAD⊥平面ABCD;
(2)求点C到平面PDB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 为两两不重合的平面,
为两两不重合的平面,![]() ,
,![]() ,
,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中真命题是( )
A.①③B.②④C.③④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为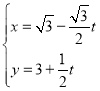 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,过极点
轴的正半轴为极轴的极坐标系中,过极点![]() 的射线与曲线
的射线与曲线![]() 相交于不同于极点的点
相交于不同于极点的点![]() ,且点
,且点![]() 的极坐标为
的极坐标为![]() ,其中
,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若射线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
(Ⅰ)试确定点F的位置,使得直线EF∥平面PDC;
(Ⅱ)若PB=3BF,求直线AF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极稳妥疫情期间的复学工作,市教育局抽调5名机关工作人员去某街道3所不同的学校开展驻点服务,每个学校至少去1人,若甲、乙两人不能去同一所学校,则不同的分配方法种数为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com