
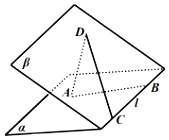
【题目】如图所示的多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
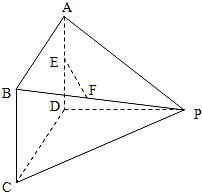
(Ⅰ)试确定点F的位置,使得直线EF∥平面PDC;
(Ⅱ)若PB=3BF,求直线AF与平面PBC所成角的正弦值.
【答案】(Ⅰ)当点F为BP中点时,使得直线EF∥平面PDC;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设F为BP中点,取AP中点G,连结EF、EG、FG,推导出GF∥AB∥CD,EG∥DP,从而平面GEF∥平面PDC,进而当点F为BP中点时,使得直线EF∥平面PDC.
(Ⅱ)以D为原点,DC为x轴,在平面PDC中过D作CD垂线为y轴,DA为z轴,建立空间直角坐标系,求得平面PBC的一个法向量,![]() 的坐标,代入公式sinθ
的坐标,代入公式sinθ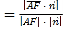 求解.
求解.
(Ⅰ)设F为BP中点,取AP中点G,连结EF、EG、FG,
∵AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,
∴GF∥AB∥CD,EG∥DP,
∵EG∩FG=G,DP∩CD=D,∴平面GEF∥平面PDC,
∵EF平面GEF,
∴当点F为BP中点时,使得直线EF∥平面PDC.
(Ⅱ)以D为原点,DC为x轴,在平面PDC中过D作CD垂线为y轴,DA为z轴,建立空间直角坐标系,

∵E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
∴cos120°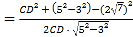 ,解得CD=2,
,解得CD=2,
所以A(0,0,3),B(2,0,3),P(﹣2,2![]() ,0),C(2,0,0),
,0),C(2,0,0),
设F(a,b,c),由PB=3BF,得![]() ,
,
即(a﹣2,b,c﹣3)![]() (﹣8,2
(﹣8,2![]() ,﹣3),
,﹣3),
解得a![]() ,b
,b![]() ,c=2,∴F(
,c=2,∴F(![]() ,
,![]() ,2),
,2),
![]() (
(![]() ,﹣1),
,﹣1),![]() (0,0,3),
(0,0,3),![]() (﹣4,2
(﹣4,2![]() ,0),
,0),
设平面PBC的一个法向量![]() (x,y,z),
(x,y,z),
则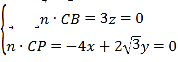 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ,0),
,0),
设直线AF与平面PBC所成角为θ,
则直线AF与平面PBC所成角的正弦值为:
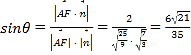 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知平面![]() ,B,
,B,![]() ,
,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,则下列叙述错误的是( )
,则下列叙述错误的是( )
A.直线![]() 与
与![]() 是异面直线
是异面直线
B.直线![]() 在
在![]() 上的射影可能与
上的射影可能与![]() 平行
平行
C.过![]() 有且只有一个平面与
有且只有一个平面与![]() 平行
平行
D.过![]() 有且只有一个平面与
有且只有一个平面与![]() 垂直
垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在平面五边形![]() 中,
中,![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是等边三角形.现将
是等边三角形.现将![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 得如图②的几何体.
得如图②的几何体.
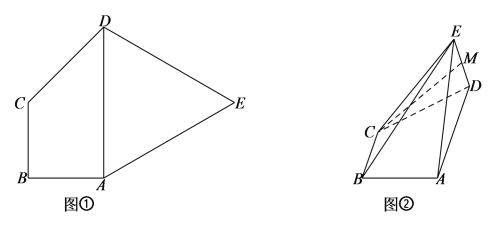
(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某地5月1日至15日日平均温度变化的折线图,日平均温度高于20度低于27度时适宜户外活动,某人随机选择5月1日至5月14日中的某一天到达该地停留两天(包括到达当日).
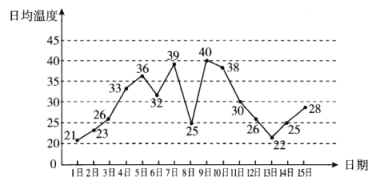
(1)求这15天日平均温度的极差和均值;
(2)求此人停留期间只有一天的日平均温度适宜户外活动的概率;
(3)由折线图判断从哪天开始连续三天日平均温度的方差最大?(写出结论,不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com