
【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,四边形ABCD是边长为2的正方形,△PAD为等边三角形,E,F分别为PC和BD的中点,且EF⊥CD.
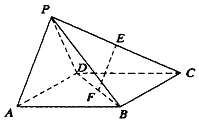
(1)证明:平面PAD⊥平面ABCD;
(2)求点C到平面PDB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为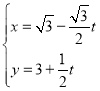 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,过极点
轴的正半轴为极轴的极坐标系中,过极点![]() 的射线与曲线
的射线与曲线![]() 相交于不同于极点的点
相交于不同于极点的点![]() ,且点
,且点![]() 的极坐标为
的极坐标为![]() ,其中
,其中![]() .
.
(1)求![]() 的值;
的值;
(2)若射线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 在
在![]() 轴正半轴及
轴正半轴及![]() 轴正半轴截距相等时的直角坐标方程;
轴正半轴截距相等时的直角坐标方程;
(2)若![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,点
,点![]() ,求
,求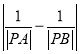 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
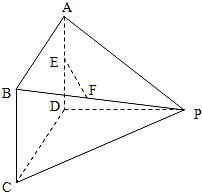
(Ⅰ)试确定点F的位置,使得直线EF∥平面PDC;
(Ⅱ)若PB=3BF,求直线AF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是梯形,
是梯形,![]() //
//![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 是
是![]() 上的动点.
上的动点.
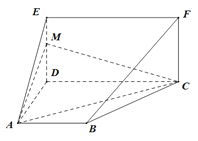
(1)试确定![]() 点的位置,使
点的位置,使![]() //平面
//平面![]() ;
;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com