【题目】已知平面
，B，
，
，且
，
，且
，则下列叙述错误的是（ ）
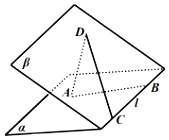
A.直线
与
是异面直线
B.直线
在
上的射影可能与
平行
C.过有且只有一个平面与平行
D.过有且只有一个平面与垂直
【答案】D
【解析】
利用反证法判断选项
正确；举例说明选项
正确；由公理3的推论结合过直线外一点有且只有一条直线与已知直线平行判断选项
正确；由异面直线垂直及线面关系判断选项
错误．
对于选项，若直线
与
是共面直线，设与共面
，
不共线的三点，，均在
与内，
与重合，
又不共线的三点，，均在
与内，
与重合，则与重合，与
矛盾，
故直线与是异面直线，所以选项正确；
对于选项，当
，
，且二面角
为锐二面角时，直线
在上的射影与
平行，所以选项正确；
对于选项，在上任取一点，过该点作的平行线
，则由与确定一个平面，该平面与平行，
若过另外有平面与平行，由直线与平面平行的性质，可得过直线外的一点有两条直线与平行，
与过直线外一点有且只有一条直线与已知直线平行矛盾，所以选项正确；
对于选项，只有当与异面垂直时，过有且只有一个平面与，否则，不存在过与垂直的平面，故选项错误．
故选：D．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程是：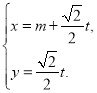
（
是参数）.以原点
为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程是
.
（1）若直线与曲线相交于
两点，且
，试求实数
值；
（2）设
为曲线上任意一点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
如图，在四面体
中，
、
分别是
、
的中点，
、
分别是
和
上的动点，且
与
相交于点
．下列判断中：
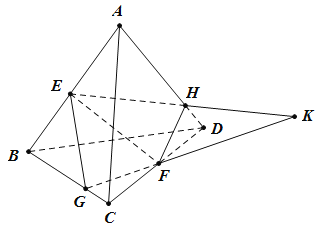
①直线
经过点；
②
；
③、、、四点共面，且该平面把四面体的体积分为相等的两部分．
所有正确的序号为
__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方形
的边长为2，
分别为线段
的中点，在五棱锥
中，
为棱
的中点，平面
与棱
分别交于点
．
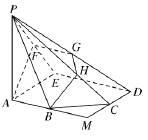
（1）求证：
；
（2）若
底面
，且
，求直线
与平面
所成角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，四边形ABCD是边长为2的正方形，△PAD为等边三角形，E，F分别为PC和BD的中点，且EF⊥CD．
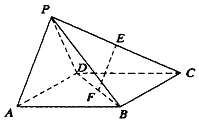
（1）证明：平面PAD⊥平面ABCD；
（2）求点C到平面PDB的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示的多面体中，AD⊥平面PDC，四边形ABCD为平行四边形，E为AD的中点，F为线段PB上的一点，∠CDP＝120°，AD＝3，AP＝5，
．
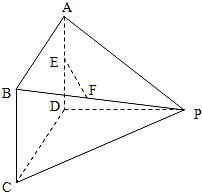
（Ⅰ）试确定点F的位置，使得直线EF∥平面PDC；
（Ⅱ）若PB＝3BF，求直线AF与平面PBC所成角的正弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
