
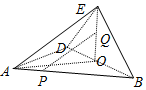
 在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.
在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.分析 (Ⅰ)证明PR∥平面ADE,RQ∥平面ADE,可得平面PQR∥平面ADE,即可证明:直线PQ∥平面ADE;
(Ⅱ)由等体积法可得点O到平面ADE的距离,即可求直线BD与平面ADE所成角θ的正弦值.
解答 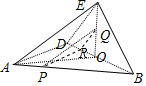 (Ⅰ)证明:如图,取OD的中点R,连接PR,QR,则DE∥RQ,
(Ⅰ)证明:如图,取OD的中点R,连接PR,QR,则DE∥RQ,
由题知$AB=4\sqrt{2}$,又$AP=\sqrt{2}$,故AB:AP=4:1=DB:DR,因此AD∥PR,
因为PR,RQ?平面ADE,
且AD,DE?平面ADE,故PR∥平面ADE,RQ∥平面ADE,
又PR∩RQ=R,
故平面PQR∥平面ADE,从而PQ∥平面ADE.…6分
(Ⅱ)解:由题EA=ED=5,$AD=4\sqrt{2}$,设点O到平面ADE的距离为d,
则由等体积法可得$\frac{1}{3}•\frac{1}{2}•4\sqrt{2}$$•\sqrt{25-8}•d=\frac{1}{3}•\frac{1}{2}•4•4•3$,
故$d=\frac{{6\sqrt{34}}}{17}$,因此$sinθ=\frac{d}{OD}=\frac{3}{34}\sqrt{34}$.…12分.
点评 本题考查线面平行的判定,考查线面角,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
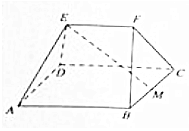 如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.
如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF=$2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$+2 | B. | $\frac{π}{3}$+$\frac{2}{3}$ | C. | π$+\frac{2}{3}$ | D. | π+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
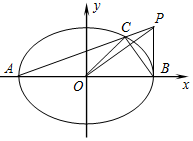 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com