
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB//CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
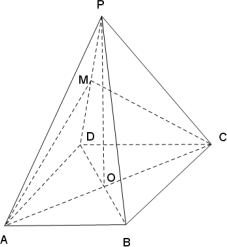
(Ⅰ)证明:PD⊥AC;
(Ⅱ)求二面角A-PB-D的大小;
(Ⅲ)若DM∶MP=k,则当k为何值时直线PD⊥平面ACM?
|
解(Ⅰ)∵PO⊥平面ABCD, ∴DO为DP在平面ABCD内的射影. 1分 又∵AC⊥BD, ∴AC⊥PD. 3分 (Ⅱ)方法1: 过O作ON⊥PB于N,连结AN. ∵PO⊥平面ABCD, 又AO ∴PO⊥AO. 4分 由已知AO⊥BD,BD∩PO=O, ∴AO⊥平面PBD. 5分 ∴ON为AN在平面PBD内的射影, ∴PB⊥AN. ∴∠ANO为二面角A-PB-D的平面角. 6分
在Rt△AOD中,AO=1. ∵PO⊥平面ABCD, ∴OA为PA在底面ABCD内的射影. ∴∠PAO为直线PA与底面ABCD所成的角,∠PAO=60°. 7分 ∴在Rt△POA中,PO= ∵四边形ABCD为等腰梯形, ∴△ABD≌△BAC, ∴∠ABD=∠BAC, ∴OA=OB=1. 8分 在Rt△POB中,PB=2. ∴ON= 在Rt△AON中, tan∠ANO= ∴二面角A-PB-D的大小为arctan
方法2: 如图,以O为坐标原点,OB,OC,OP所在直线分别为 A(0,-1,0),B(1,0,0), P(0,0, ∵PO⊥平面ABCD, 又AO ∴PO⊥AO. 由已知AO⊥BD,BD∩PO=O, ∴AO⊥平面PBD. ∴ 设 则 ∴二面角A-PB-D的大小为arccos
(Ⅲ)当DM∶MP=1时,直线PD⊥平面ACM. 11分 ∵PO⊥平面ABCD, ∴OA为PRA在底面ABCD内的射影. ∴∠PAO为直线PA与底面ABCD所成的角,∠PAO= 又∵在Rt△AOD中,∠DAO=60°, ∴Rt△AOD≌Rt△AOP. ∴AD=AP. ∵PM=MD, ∴PD⊥AM. 13分 由(Ⅰ)可知PD⊥AC. ∵AM ∴直线PD⊥平面ACM. 14分 |


科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且PD=a,PA=PC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
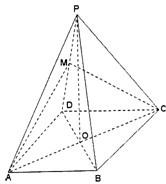 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com