
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点.设直线
两点.设直线![]() 是抛物线
是抛物线![]() 的切线,且直线
的切线,且直线![]() 为
为![]() 上一点,且
上一点,且![]() 的最小值为
的最小值为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 是抛物线
是抛物线![]() 上,分别位于
上,分别位于![]() 轴两侧的两个动点,
轴两侧的两个动点,![]() 为坐标原点,且
为坐标原点,且![]() .求证:直线
.求证:直线![]() 必过定点,并求出该定点的坐标.
必过定点,并求出该定点的坐标.
【答案】(1)![]() (2)见解析,
(2)见解析,![]() .
.
【解析】
(1)依题意,设出M、N坐标及直线![]() 的方程为
的方程为![]() ,代入抛物线方程,可得根与系数关系,设直线
,代入抛物线方程,可得根与系数关系,设直线![]() 和抛物线
和抛物线![]() 相切于点
相切于点![]() ,由题意和切线的几何意义知,曲线
,由题意和切线的几何意义知,曲线![]() 在
在![]() 处的切线斜率为1,因此得
处的切线斜率为1,因此得![]() ,可得切线
,可得切线![]() 的方程,设出P点坐标,代入
的方程,设出P点坐标,代入![]() 化简并求得最小值为
化简并求得最小值为![]() 可解出p,即可求抛物线C的方程,并求其准线方程;
可解出p,即可求抛物线C的方程,并求其准线方程;
(2)直线![]() 的斜率一定存在,设
的斜率一定存在,设![]() 的方程为
的方程为![]() ,代入y2=4x,利用韦达定理结合
,代入y2=4x,利用韦达定理结合![]() ,求出b,即可证明直线l必过一定点,并求出该定点.
,求出b,即可证明直线l必过一定点,并求出该定点.
(1)依题意,直线![]() 的方程为
的方程为![]() .
.
设![]() ,
,
将直线![]() 的方程代入
的方程代入![]() 中,
中,
得![]() ,
,
因此![]() .
.
设直线![]() 和抛物线
和抛物线![]() 相切于点
相切于点![]() ,
,
由题意和切线的几何意义知,曲线![]() 在
在![]() 处的切线斜率即导数为1,
处的切线斜率即导数为1,
因此得![]() ,
,
![]() 切点
切点![]() 的坐标为
的坐标为![]() ,
,
因此切线![]() 的方程为
的方程为![]() .
.
设![]() ,
,
于是![]()
![]()
![]()
将![]() ,
,![]() 代入其中,
代入其中,
可得![]() .
.
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
由![]() ,
,
可解得正数![]() 值为2,
值为2,
因此所求的抛物线方程为![]() .
.
(2)显然,直线![]() 的斜率一定存在,
的斜率一定存在,
设![]() 的方程为
的方程为![]() ,
,![]() ,
,
则![]() ,
,
故![]() ,
,
也即![]() ,①
,①
将![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() ,
,
故![]() .
.
将它们代入到①中,得![]() ,
,
解得![]() ,
,
因此直线![]() 恒过点
恒过点![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有唯一一个整数,则实数
的解集中恰有唯一一个整数,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图统计了截止2019年年底中国电动车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
中国电动车充电桩细分产品占比情况:
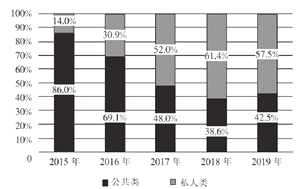
中国电动车充电桩细分产品保有量情况:(单位:万台)
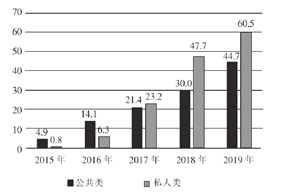
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列(![]() )又称黄金分割数列,因数学家列昂纳多斐波那契(
)又称黄金分割数列,因数学家列昂纳多斐波那契(![]() )以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列
)以兔子繁殖为例子而引入,故又称为“兔子数列”.在数学上,斐波纳契数列被以下递推的方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
,现从数列的前2024项中随机抽取1项,能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x,直线l交于A,B两点,O为坐标原点,直线OA,OB的斜率分别为k1,k2,若k1k2=﹣2,则△AOB面积的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若直线![]() 且曲线
且曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,求a的取值范围;
在B处的切线相互平行,求a的取值范围;
(Ⅱ)设![]() 在其定义域内有两个不同的极值点
在其定义域内有两个不同的极值点![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥PABC的各顶点都在同一球面上,![]() 底面ABC,若
底面ABC,若![]() ,
,![]() ,且
,且![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.![]() 是钝角三角形B.此球的表面积等于
是钝角三角形B.此球的表面积等于![]()
C.![]() 平面PACD.三棱锥APBC的体积为
平面PACD.三棱锥APBC的体积为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com