考点:导数在最大值、最小值问题中的应用,两角和与差的正弦函数,正弦函数的定义域和值域
专题:导数的综合应用,三角函数的图像与性质
分析:(1)利用辅助角公式,我们可以确定函数y=f (sinx+
cosx)(x∈R)的解析式,进而利用换无法,可将问题转化了一个二次函数在定区间上的最值问题,进而得到答案.
(2)由x∈R,x≠kπ且x≠kπ+
,利用换元法我们可以将不等与左边对应的函数转化为f(t)=tlog
2t+(1-t)log
2(1-t),进而根据二次函数的性质,判断出其最值,并将问题转化为一个函数恒成立问题,最后得到结论.
解答:
(1)解:令
t=sinx+cosx=2sin(x+),
∵x∈R,∴-2≤t≤2,----2分
∴
y=t2+at=(t+)2-,
当a<0时,t=-2时,
y最大=4-2a=,解得:
a=-此时
f(x)=(x-)2-,∴
f(x)最小值=-.--------2分
当a≥0时,t=2时,
y最大=4+2a=,解得:
a=此时,
f(x)=(x+)2-,∴
f(x)最小值=-综合上述,条件满足时,f(x)的最小值为
--------2分
(2)证明:∵x∈R,x≠kπ且
x≠kπ+(k∈Z),∴sin
2x,cos
2x∈(0,1)
又sin
2x+cos
2x=1,故设t=sin
2x,则有cos
2x=1-t
设f(t)=tlog
2t+(1-t)log
2(1-t)(其中t∈(0,1))------------2分
∴
f′(t)=log2t+log2e-log2(1-t)-log2e=log2----------2分
令f'(t)=0,得
t=当
0<t<时,f'(t)<0,∴f(t)在(0,
)单调递减,
当
<t<1时,f'(t)>0,∴f(t)在(
,1)单调递增,
∴
t=时f(t)取最小值等于
f()=log2+log2=log2=-1,
即有
sin2xlog2sin2x+cos2xlog2cos2x≥-1----------3分
当a>2时,f(x)=x
2+ax的对称轴
x=-<-1,∴f(x)在(-1,+∞)上单调递增,
∴
f(sin2xlog2sin2x+cos2xlog2cos2x)≥f(-1)=1-a-------2分.
点评:本题考查的知识点是二次函数在闭区间上的最值,不等式的综合,三角函数的最值,熟练掌握二次函数的性质是解答本题的关键.



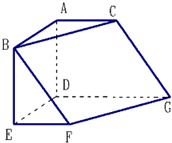 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.