

| A�� | ���ڵı仯������С��������ƽ���۸���� | |
| B�� | ���ں����ŵĴ����ڼ�������Ʊ�۸�ͬȥ����������½� | |
| C�� | ƽ���۸�Ӹߵ��;���ǰ��λ�ij���Ϊ���������ڡ����� | |
| D�� | ƽ���۸�仯���Ӹߵ��;���ǰ��λ�ij���Ϊ������������� |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ͼ�����ֱ��$x=-\frac{��}{4}$�Գ� | |
| B�� | ��ͼ�����$y=2sin��x+\frac{��}{4}��+1$ͼ�������е�ĺ������Ϊԭ����$\frac{1}{3}$���õ� | |
| C�� | ��ͼ����ڵ�$��\frac{11��}{12}��0��$�Գ� | |
| D�� | ��ֵ����[-1��3] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ˫����$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1�Ľ��㵽�佥���߾���Ϊ$\sqrt{3}$ | |
| B�� | ������p��?x��R��ʹ��sinx+cosx��2����Vp��?x��R������sinx+cosx��2 | |
| C�� | ��p��q�Ǽ����⣬��p��q���Ǽ����� | |
| D�� | ��a��b�ǻ�����ֱ����������ֱ�ߣ������Ψһƽ�����ʹ��a?������b�Φ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����Ϻ��������и���9���¿���ѧ���ģ��Ծ��������棩 ���ͣ�ѡ����
��֪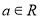 ����
����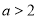 ���ǡ�
���ǡ�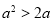 ���ģ� ��
���ģ� ��
A����ַDZ����� B����Ҫ���������
C����Ҫ���� D���ȷdz��Ҳ�DZ�Ҫ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com