
| A. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1的焦点到其渐近线距离为$\sqrt{3}$ | |
| B. | 若命题p:?x∈R,使得sinx+cosx≥2,则¬p:?x∈R,都有sinx+cosx<2 | |
| C. | 若p∧q是假命题,则p、q都是假命题 | |
| D. | 设a,b是互不垂直的两条异面直线,则存在唯一平面α,使得a?α,且b∥α |
分析 由双曲线的焦点坐标和渐近线方程,结合点到直线的距离公式,计算判断A;由特称命题的否定为全称命题,可判断B;由复合命题的真值表,可判断C;运用正方体模型,即可判断D.
解答 解:A,双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1的焦点($\sqrt{5}$,0)到其渐近线$\sqrt{3}$x-$\sqrt{2}$y=0距离为d=$\frac{|\sqrt{3}•\sqrt{5}-0|}{\sqrt{3+2}}$=$\sqrt{3}$,故A正确;
B,若命题p:?x∈R,使得sinx+cosx≥2,则¬p:?x∈R,都有sinx+cosx<2,由命题的否定形式,故B正确;
C,若p∧q是假命题,则p、q中至少有一个为假命题,故C不正确;
D,设a,b是互不垂直的两条异面直线,由a,b是互不垂直的两条异面直线,把它放入正方体中如图;
则存在唯一平面α,使得a?α,且b∥α,故D正确.
故选:C.
点评 本题考查命题的真假判断和运用,考查双曲线的方程和性质,空间线线和线面的位置关系以及复合命题的真假及命题的否定形式,考查判断推理和空间想象能力,属于基础题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 深圳的变化幅度最小,北京的平均价格最高 | |
| B. | 深圳和厦门的春运期间往返机票价格同去年相比有所下降 | |
| C. | 平均价格从高到低居于前三位的城市为北京、深圳、广州 | |
| D. | 平均价格变化量从高到低居于前三位的城市为天津、西安、厦门 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,0) | C. | (0,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知点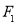 、
、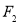 是双曲线
是双曲线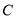 :
: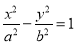 (
(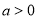 ,
,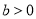 )的左、右焦点,
)的左、右焦点,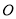 为坐标原点,点
为坐标原点,点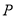 在双曲线
在双曲线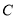 的右支上,且满足
的右支上,且满足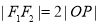 ,
,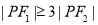 ,则双曲线
,则双曲线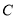 的离心率的取值范围为( )
的离心率的取值范围为( )
A.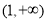 B.
B.
C.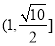 D.
D.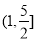
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:填空题
已知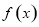 是定义在
是定义在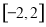 上的奇函数,当
上的奇函数,当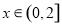 时,
时,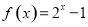 ,函数
,函数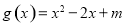 ,如果对于
,如果对于 ,使得
,使得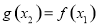 ,则实数
,则实数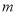 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com