
分析 (1)方案乙中所需化验次数恰好为2次的事件有两种情况:第一种,先化验一组,结果不含病毒DNA,再从另一组任取一个样品进行化验,可得恰含有病毒的概率为$\frac{{∁}_{5}^{2}}{{∁}_{6}^{3}}$×$\frac{1}{{∁}_{3}^{1}}$.第二种,先化验一组,结果含有病毒DNA,再从中逐个化验,恰第一个样品含有病毒的概率为$\frac{{∁}_{5}^{2}}{{∁}_{6}^{3}}$×$\frac{1}{{∁}_{3}^{1}}$.利用互斥事件的概率计算公式即可得出.
(2)设方案甲化验的次数为ξ,则ξ可能的取值为1,2,3,4,5,对应的化验费为η元,利用相互独立事件的概率计算公式可得:P(ξ=1)=P(η=10),P(ξ=2)=P(η=18),P(ξ=3)=P(η=24),P(ξ=4)=P(η=30),P(ξ=5)=P(η=36).
解答 解:(1)方案乙中所需化验次数恰好为2次的事件有两种情况:
第一种,先化验一组,结果不含病毒DNA,再从另一组任取一个样品进行化验,
则恰含有病毒的概率为$\frac{{∁}_{5}^{2}}{{∁}_{6}^{3}}$×$\frac{1}{{∁}_{3}^{1}}$=$\frac{1}{6}$.
第二种,先化验一组,结果含有病毒DNA,再从中逐个化验,
恰第一个样品含有病毒的概率为$\frac{{∁}_{5}^{2}}{{∁}_{6}^{3}}$×$\frac{1}{{∁}_{3}^{1}}$=$\frac{1}{6}$.
∴依据方案乙所需化验恰好为2次的概率为$\frac{1}{6}+\frac{1}{6}$=$\frac{1}{3}$.
(2)设方案甲化验的次数为ξ,则ξ可能的取值为1,2,3,4,5,对应的化验费为η元,
P(ξ=1)=P(η=10)=$\frac{1}{6}$,
P(ξ=2)=P(η=18)=$\frac{5}{6}$×$\frac{1}{5}$=$\frac{1}{6}$,
P(ξ=3)=P(η=24)=$\frac{5}{6}×$$\frac{4}{5}$×$\frac{1}{4}$=$\frac{1}{6}$,
P(ξ=4)=P(η=30)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{1}{3}$=$\frac{1}{6}$,
P(ξ=5)=P(η=36)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}$=$\frac{1}{3}$,
∴方案甲所需化验费用η的分布列为:
| η | 10 | 18 | 24 | 30 | 36 |
| P | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{3}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望计算公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$或0 | B. | $\frac{4}{3}$或0 | C. | -$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ex+e-x | B. | y=ln(|x|+1) | C. | $y=\frac{sinx}{|x|}$ | D. | $y=x-\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 深圳的变化幅度最小,北京的平均价格最高 | |
| B. | 深圳和厦门的春运期间往返机票价格同去年相比有所下降 | |
| C. | 平均价格从高到低居于前三位的城市为北京、深圳、广州 | |
| D. | 平均价格变化量从高到低居于前三位的城市为天津、西安、厦门 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知点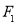 、
、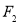 是双曲线
是双曲线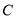 :
: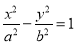 (
(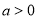 ,
,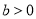 )的左、右焦点,
)的左、右焦点,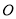 为坐标原点,点
为坐标原点,点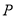 在双曲线
在双曲线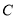 的右支上,且满足
的右支上,且满足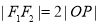 ,
,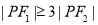 ,则双曲线
,则双曲线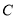 的离心率的取值范围为( )
的离心率的取值范围为( )
A.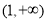 B.
B.
C.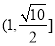 D.
D.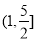
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com