
分析 直线MN的方程为y=k(x-1),代入抛物线方程可得k2x2-(2k2+4)x+k2=0,求出k的值可得M的坐标,即可得出结论.
解答 解:设M(x1,y1),N(x2,y2),直线MN的方程为y=k(x-1),代入抛物线方程可得k2x2-(2k2+4)x+k2=0
∴x1+x2=2+$\frac{4}{{k}^{2}}$,
2|FN|=|MD|,可得2(x2+1)=|MD|,
∵$\frac{MD}{MF}=\frac{MQ}{MP}$,∴$\frac{2({x}_{2}+1)}{{x}_{1}+1}$=$\frac{{x}_{1}}{{x}_{1}+1}$,∴x2=$\frac{1}{2}{x}_{1}$-1,
联立可得x1=2+$\frac{8}{3{k}^{2}}$,
∵x1=$\frac{{k}^{2}+2+2\sqrt{1+{k}^{2}}}{{k}^{2}}$,
∴2+$\frac{8}{3{k}^{2}}$=$\frac{{k}^{2}+2+2\sqrt{1+{k}^{2}}}{{k}^{2}}$,
∴3k2=4$\sqrt{3}$+4,
∴x1=$\sqrt{3}$+1,
∴|MF|=$\sqrt{3}$+2,
故答案为$\sqrt{3}$+2.
点评 本题考查抛物线的方程与性质,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
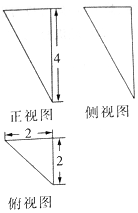
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{6}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2} | C. | {1,2,5,6} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)•g(sinB)>f(sinB)•g(sinA) | B. | f(sinA)•g(sinB)<f(sinB)•g(sinA) | ||
| C. | f(cosA)•g(sinB)>f(sinB)•g(cosA) | D. | f(cosA)•g(sinB)<f(sinB)•g(cosA) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com