
| A. | y=ex+e-x | B. | y=ln(|x|+1) | C. | $y=\frac{sinx}{|x|}$ | D. | $y=x-\frac{1}{x}$ |
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2} | C. | {1,2,5,6} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)•g(sinB)>f(sinB)•g(sinA) | B. | f(sinA)•g(sinB)<f(sinB)•g(sinA) | ||
| C. | f(cosA)•g(sinB)>f(sinB)•g(cosA) | D. | f(cosA)•g(sinB)<f(sinB)•g(cosA) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 其图象关于直线$x=-\frac{π}{4}$对称 | |
| B. | 其图象可由$y=2sin(x+\frac{π}{4})+1$图象上所有点的横坐标变为原来的$\frac{1}{3}$倍得到 | |
| C. | 其图象关于点$(\frac{11π}{12},0)$对称 | |
| D. | 其值域是[-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知函数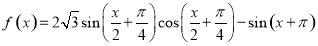 .
.
(1)求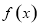 的最小正周期;
的最小正周期;
(2)若将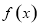 的图象向右平移
的图象向右平移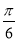 个单位,得到函数
个单位,得到函数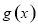 的图象,求函数
的图象,求函数 在区间
在区间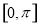 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com