
分析 由对于任意非零实数m,不等式|2m-1|+|1-m|≥|m|(|x-1|-|2x+3|)恒成立,即|x-1-|2x-3|≤$\frac{|2m-1|+|1-m|}{|m|}$恒成立,由$\frac{|2m-1|+|1-m|}{|m|}$≥$\frac{|2m-1+1-m|}{|m|}$=1,因此只需|x-1|-|2x+3|≤1.对x分类讨论解出即可得出x的取值范围.
解答 解:由对于任意非零实数m,不等式|2m-1|+|1-m|≥|m|(|x-1|-|2x+3|)恒成立,
即|x-1-|2x-3|≤$\frac{|2m-1|+|1-m|}{|m|}$恒成立,
∵$\frac{|2m-1|+|1-m|}{|m|}$≥$\frac{|2m-1+1-m|}{|m|}$=1,
∴只需|x-1|-|2x+3|≤1.
①当x$≤-\frac{3}{2}$时,原式1-x+2x+3≤1,即x≤-3,所以x≤-3
②当$-\frac{3}{2}<x<1$时,原式1-x-2x-3≤1,即x≥-1,所以-1≤x<1
③当x≥1时,原式x-1-2x-3≤1,即x≥-5,所以x≥1.
综上x的取值范围为(-∞,-3]∪[-1,+∞).
点评 本题考查了绝对值不等式的解法、恒成立问题的等价转化方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.
如图所示,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
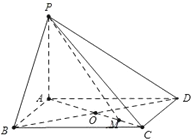 已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=120°,PA=3.
已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=120°,PA=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com