
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
资源 消耗量 产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤( | 9 | 4 | 360 |
电力( | 4 | 5 | 200 |
劳力(个) | 3 | 10 | 300 |
利润(万元) | 7 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 为
为![]() 上任意两点,且
上任意两点,且![]() 的长为定值,则下面的四个值中不为定值的是( )
的长为定值,则下面的四个值中不为定值的是( )
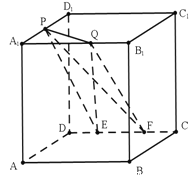
A. 点![]() 到平面
到平面![]() 的距离B. 三棱锥
的距离B. 三棱锥![]() 的体积
的体积
C. 直线![]() 与平面
与平面![]() 所成的角D. 二面角
所成的角D. 二面角![]() 的大小
的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
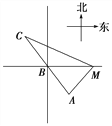
【题目】如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于1 km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则
,则
(![]() )函数
)函数![]() 定义域为__________.
定义域为__________.
(![]() )函数
)函数![]() 导函数为
导函数为![]() __________.
__________.
(![]() )对函数
)对函数![]() 单调研究如下
单调研究如下
| |||||
|
|
| |||
|
____
(![]() )设函数
)设函数 则
则
函数![]() 的最大值为__________.
的最大值为__________.
(5)函数![]() 极值点共__________个,(6)其中极小值点有__________个.
极值点共__________个,(6)其中极小值点有__________个.
(7)若关于![]() 的方程
的方程![]() 恰有三个不相同的实数解,则
恰有三个不相同的实数解,则![]() 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.

(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
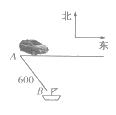
【题目】如图所示,一辆汽车从![]() 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以![]() 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在![]() 市南偏东30°方向距
市南偏东30°方向距![]() 市
市![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.问快艇至少以多大的速度,以什么样的航向行驶才能最快把稿件送到司机手中?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com