
分析 ①根据$\overrightarrow{α}$与$\overrightarrow{β}$的夹角为120°,结合向量加法的三角形法则,及连接直线上的点与直线外一点的线段中,垂线段最短得到当t|$\overrightarrow{β}$-$\overrightarrow{α}$|=$\frac{1}{2}$时,|(1-t)$\overrightarrow α$+t$\overrightarrow β}$|取最小值;
②由$\overrightarrow{a}$•$\overrightarrow{b}$=0得出$\overrightarrow{a}$⊥$\overrightarrow{b}$,建立直角坐标系,设$\overrightarrow{a}$=(m,0),$\overrightarrow{b}$=(0,n),$\overrightarrow{c}$=(x,y),根据|$\overrightarrow{a}$-$\overrightarrow{b}$|=5得m2+n2=25,记此圆为⊙M;
根据向量$\overrightarrow{c}$满足($\overrightarrow{c}$-$\overrightarrow{a}$)($\overrightarrow{c}$-$\overrightarrow{b}$)=0,说明点C在⊙M上;
由|$\overrightarrow{AC}$|=|$\overrightarrow{c}$-$\overrightarrow{a}$|=3,|$\overrightarrow{BC}$|=|$\overrightarrow{c}$-$\overrightarrow{b}$|=4,过点C分别作CD⊥y轴,
设∠CBD=θ,可得x=4sinθ=m-3cosθ,$\overrightarrow{a}$•$\overrightarrow{c}$=mx=10sin(2θ-φ)+8,从而求得结论.
解答 解:①∵平面向量$\overrightarrow{α}$满足|$\overrightarrow{α}$|=2,且$\overrightarrow{α}$与$\overrightarrow{β}$-$\overrightarrow{α}$的夹角为120°,
故当t($\overrightarrow{β}$-$\overrightarrow{α}$)满足t|$\overrightarrow{β}$-$\overrightarrow{α}$|=$\frac{1}{2}$时,|(1-t)$\overrightarrow{a}$+t$\overrightarrow{β}$|(t∈R)取最小值,
此时由向量加法的三角形法则可得|(1-t)$\overrightarrow{α}$+$\overrightarrow{β}$|(t∈R)的最小值是$\sqrt{3}$;
②由$\overrightarrow{a}$•$\overrightarrow{c}$=0,建立如图所示的直角坐标系;
可设$\overrightarrow{a}$=(m,0),$\overrightarrow{b}$=(0,n),$\overrightarrow{c}$=(x,y),
∵|$\overrightarrow{a}$-$\overrightarrow{b}$|=5,
∴m2+n2=25,记此圆为⊙M;
∵向量$\overrightarrow{c}$满足($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=0,
∴x2+y2-mx-ny=0,
化为${(x-\frac{m}{2})}^{2}$+${(y-\frac{n}{2})}^{2}$=$\frac{25}{4}$,
说明点C在⊙M上;
∴|$\overrightarrow{AC}$|=|$\overrightarrow{c}$-$\overrightarrow{a}$|=3,
∴|$\overrightarrow{BC}$|=|$\overrightarrow{c}$-$\overrightarrow{b}$|=4,
过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E;
设∠CBD=θ,则∠OAC=θ,
则x=4sinθ=m-3cosθ,
∵$\overrightarrow{a}$•$\overrightarrow{c}$=mx=4sinθ(4sinθ+3cosθ)
=16sin2θ+12sinθcosθ
=8(1-cos2θ)+6sin2θ
=10sin(2θ-φ)+8≤18;
∴$\overrightarrow{a}$•$\overrightarrow{c}$的最大值为18.
故答案为:$\sqrt{3}$,18.
点评 本题考查了向量的模以及向量在几何中的应用问题,也考查了向量的坐标运算、向量垂直与数量积的应用问题,是综合性题目.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{-\sqrt{7}}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | ($\frac{-1}{2}$,$\frac{1}{2}$) | D. | ($\frac{-1+\sqrt{7}}{2}$,$\frac{1+\sqrt{3}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
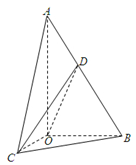 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com