
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点F1,F2,且过椭圆一个焦点及顶点的直线方程为x-y+$\sqrt{3}$=0
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点F1,F2,且过椭圆一个焦点及顶点的直线方程为x-y+$\sqrt{3}$=0分析 (1)推导出左焦点为(-$\sqrt{3}$,0),上顶点为(0,$\sqrt{3}$),从而能求出椭圆方程.
(2)设直线l的方程为x=my+3,直线AP的方程为:y-1=$\frac{{y}_{{1}_{\;}-1}}{{x}_{1}-2}(x-2)$,从而求出M坐标,同理,求出N点坐标,联立$\left\{\begin{array}{l}{x=my+3}\\{{x}^{2}+2{y}^{2}=6}\end{array}\right.$,得:(2+m2)y2+6my+3=0,由此利用根的判别式、韦达定理,结合已知条件能证明|CM|•|CN|=$\frac{1}{4}$.
解答 解:(1)∵过椭圆一个焦点及顶点的直线方程为x-y+$\sqrt{3}$=0,
∴左焦点为(-$\sqrt{3}$,0),上顶点为(0,$\sqrt{3}$),
∴b=c=$\sqrt{3}$,a=$\sqrt{3+3}=\sqrt{6}$,
∴椭圆方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$.
证明:(2)设直线l的方程为x=my+3,
P(x1,y1),Q(x2,y2),
直线AP的方程为:y-1=$\frac{{y}_{{1}_{\;}-1}}{{x}_{1}-2}(x-2)$,
∵过点A(2,1)的直线AP,
AQ分别与x轴相交于M,N两点,
∴M($\frac{2{y}_{1}-{x}_{1}}{{y}_{1}-1}$,0),即M($\frac{(2-m){y}_{1}-3}{{y}_{1}-1}$,0),
同理,得N($\frac{(2-m){y}_{1}-3}{{y}_{2}-1}$,0),即N($\frac{(2-m){y}_{1}-3}{{y}_{2}-1}$,0),
联立$\left\{\begin{array}{l}{x=my+3}\\{{x}^{2}+2{y}^{2}=6}\end{array}\right.$,消去x,整理,得:(2+m2)y2+6my+3=0,
由△=36m2-12(2+m2)>0,得m2>1,
${y}_{1}+{y}_{2}=-\frac{6m}{2+{m}^{2}}$,y1y2=$\frac{3}{2+{m}^{2}}$,
|CM|•|CN|=($\frac{5}{2}-\frac{(2-m){y}_{1}-3}{{y}_{1}-1}$)•($\frac{5}{2}$-$\frac{(2-m){y}_{2}-3}{{y}_{2}-1}$)
=$\frac{(1+2m){y}_{1}+3}{2({y}_{1}-1)}•\frac{(1+2m){y}_{1}+3}{2({y}_{2}-1)}$
=$\frac{(1+2m)^{2}{y}_{1}{y}_{2}+(1+2m)({y}_{1}+{y}_{2})+1}{4[{y}_{1}{y}_{2}-({y}_{1}+{y}_{2})+1]}$
=$\frac{(1+2m)^{2}•\frac{3}{2+{m}^{2}}+(1+2m)•(-\frac{6m}{2+{m}^{2}})+1}{4(\frac{3}{2+{m}^{2}}+\frac{6m}{2+{m}^{2}}+1)}$
=$\frac{3+12m+12{m}^{2}-6m-12{m}^{2}+2+{m}^{2}}{4(3+6m+2+{m}^{2})}$
=$\frac{{m}^{2}+6m+5}{4({m}^{2}+6m+5)}$=$\frac{1}{4}$.
∴|CM|•|CN|=$\frac{1}{4}$.
点评 本题考查方程的求法,考查两线段乘积为定值的证明,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“幂函数f(x)=(m2-m-1)xm在(0,+∞)上为增函数,则m=-1”为真命题 | |
| C. | 命题“若x=y则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{2}{13}\sqrt{13}$ | C. | $\frac{5}{26}\sqrt{13}$ | D. | $\frac{7}{20}\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
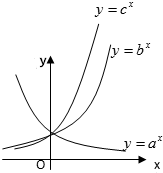
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com