
(本题满分12分)在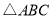 中,
中,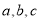 分别为角
分别为角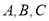 所对的边长,已知
所对的边长,已知 的周长为
的周长为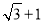 ,
, ,且
,且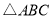 的面积为
的面积为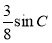 .
.
(1)求边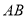 的长;
的长;
(2)求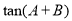 的值.
的值.
(1)1;(2) .
.
【解析】
试题分析:(1)由三角形周长得到三边之和,已知等式利用正弦定理化简得到关系式,两式联立求出AB的长即可;(2)利用三角形面积公式列出关系式,把已知面积代入求出BC•AC的值,利用余弦定理表示出cosC,利用完全平方公式变形后,把各自的值代入求出cosC的值,进而求出s1nC与tanC的值,原式利用诱导公式化简,把tanC的值代入计算即可求出值.
试题解析:(1)∵△ABC的周长为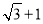 ,∴AB+BC+AC=
,∴AB+BC+AC=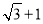 ,
,
又s1nA+s1nB= s1nC,∴由正弦定理得:BC+AC=
s1nC,∴由正弦定理得:BC+AC=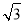 AB,
AB,
两式相减,得AB=1;
(2)由△ABC的面积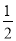 BC•ACs1nC=
BC•ACs1nC=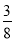 s1nC,得BC•AC=
s1nC,得BC•AC= ,
,
由余弦定理得 ,
,
又C为三角形内角,∴ ,即
,即 ,
,
则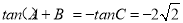 .
.
考点:正弦、余弦定理;三角形的面积公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:选择题
过抛物线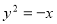 的焦点F的直线交抛物线于A、B两点,且A、B在直线
的焦点F的直线交抛物线于A、B两点,且A、B在直线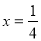 上的射影分别M、N,则∠MFN等于( )
上的射影分别M、N,则∠MFN等于( )
A.45° B.60° C.90° D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考文科数学试卷(解析版) 题型:填空题
直线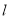 :
: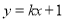 与圆
与圆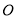 :
: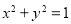 相交于
相交于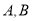 两点,则“
两点,则“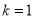 ”是“
”是“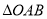 的面积为
的面积为 ”的 条件. (填写“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”之一)
”的 条件. (填写“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”之一)
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中文科数学试卷(解析版) 题型:填空题
给出以下四个命题:
①已知命题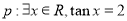 ;命题
;命题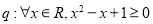 .则命题
.则命题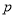 和
和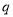 都是真命题;
都是真命题;
②过点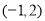 且在
且在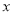 轴和
轴和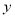 轴上的截距相等的直线方程是
轴上的截距相等的直线方程是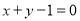 ;
;
③函数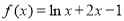 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数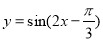 的图像向右平移
的图像向右平移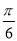 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为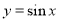 .
.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com