解:(Ⅰ)当a=2时,f(x)=x
3-6|x-1|=
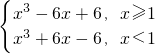
,
∴
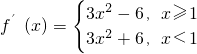
,
令f′(x)>0,得x<1或
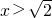
,
令f′(x)<0,得
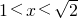
.
∵
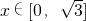
,
∴f(x)在[0,1]上单调递增,在[1,

]上单调递减,在
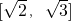
上单调递增.
∵f(0)=-6,

,
∴f(x)
min=-6.
∵f(1)=1-6+6=1,f(

)=

=6-3

<1,
∴f(x)
max=1.
(2)∵f(x)=x
3-3a|x-1|=
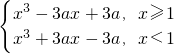
,
∴
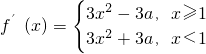
,
分类讨论如下:
①当a=0时,∵f′(x)=3x
2≥0,
∴f(x)在实数集R上单调递增;
②当a>0时,
(i)当x<1时,f′(x)=3x
2+3a>0,∴f(x)在(-∞,1)上递增;
(ii)当x≥1时.令f′(x)=0,得
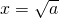
或
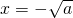
(舍),比较

与1的大小,再分类如下:
当0<a≤1时,∵f′(x)=3x
2-3a≥0,∴f(x)在(1,+∞)上递增;
当a>1时,由f′(x)=3x
2-3a<0,得1<x<

;由f′(x)=3x
2-3a≥0,得
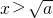
,
∴f(x)在(1,

)递减,在
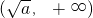
上递增.
③当a<0时,
此时,当x≥1时,f′(x)=3x
2-3a≥0,∴f(x)在(1,+∞)上递增;
当x<1时,令f′(x)=0,得
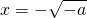
或
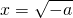
,
比较

与1的大小,再分类讨论如下:
(i)当

,即-1<a<0时,
由f′(x)=3x
2+3a>0,得
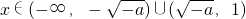
,
由f′(x)<0,得

,
∴f(x)在
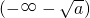
和
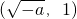
上单调递增,在
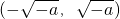
上单调递减;
(ii)当

,即a≤-1时,
由f′(x)=3x
2+3a>0,得
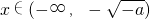
,
由f′(x)<0,得
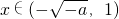
,
∴f(x)在
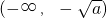
上单调递增,在
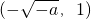
上单调递减.
综上所述:
当a>1时,f(x)在(-∞,1)上单调递增,在(
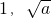
)递减,在
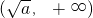
上递增;
当0≤a<1时,f(x)在R上单调递增;
当-1<a<0时,f(x)在(
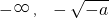
)上单调递增,在
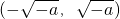
单调递减,在(
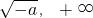
)单调递增;
当a≤-1时,f(x)在
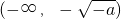
上单调递增,在(
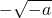
,1)上单调递减,在(1,+∞)单调递增.
分析:(Ⅰ)当a=2时,f(x)=x
3-6|x-1|=
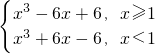
,
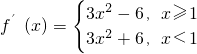
,令f′(x)>0,得x<1或
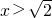
,令f′(x)<0,得
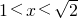
.结合
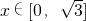
,能求出f(x)在区间x∈[0,

]上的最值.
(2)由f(x)=x
3-3a|x-1|=
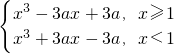
,知
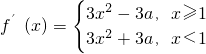
,分类讨论能求出函数f(x)的单调区间.
点评:本题考查函数最值的求法和函数的单调区间的讨论.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,仔细解答.易错点是分类不清导致出错.

 ]上的最值;
]上的最值;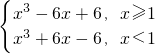 ,
,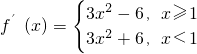 ,
,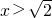 ,
,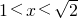 .
.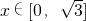 ,
, ]上单调递减,在
]上单调递减,在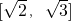 上单调递增.
上单调递增. ,
, )=
)= =6-3
=6-3 <1,
<1,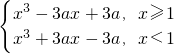 ,
,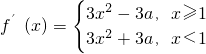 ,
,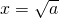 或
或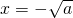 (舍),比较
(舍),比较 与1的大小,再分类如下:
与1的大小,再分类如下: ;由f′(x)=3x2-3a≥0,得
;由f′(x)=3x2-3a≥0,得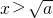 ,
, )递减,在
)递减,在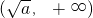 上递增.
上递增.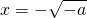 或
或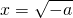 ,
, 与1的大小,再分类讨论如下:
与1的大小,再分类讨论如下: ,即-1<a<0时,
,即-1<a<0时,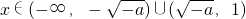 ,
, ,
,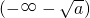 和
和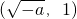 上单调递增,在
上单调递增,在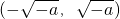 上单调递减;
上单调递减; ,即a≤-1时,
,即a≤-1时,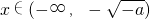 ,
,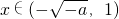 ,
,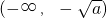 上单调递增,在
上单调递增,在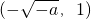 上单调递减.
上单调递减.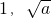 )递减,在
)递减,在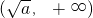 上递增;
上递增;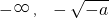 )上单调递增,在
)上单调递增,在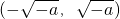 单调递减,在(
单调递减,在(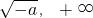 )单调递增;
)单调递增;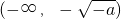 上单调递增,在(
上单调递增,在(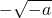 ,1)上单调递减,在(1,+∞)单调递增.
,1)上单调递减,在(1,+∞)单调递增.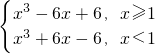 ,
,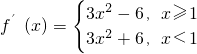 ,令f′(x)>0,得x<1或
,令f′(x)>0,得x<1或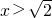 ,令f′(x)<0,得
,令f′(x)<0,得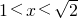 .结合
.结合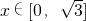 ,能求出f(x)在区间x∈[0,
,能求出f(x)在区间x∈[0, ]上的最值.
]上的最值.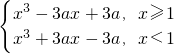 ,知
,知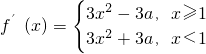 ,分类讨论能求出函数f(x)的单调区间.
,分类讨论能求出函数f(x)的单调区间.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<