
【题目】(2017·衢州调研)已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P在底面ABCD的射影,N是PC的中点.

(1)求证:平面MPB⊥平面PBC;
(2)若MP=MC,求直线BN与平面PMC所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)根据菱形性质得MB⊥BC,再根据射影定义得PM⊥平面ABCD ,即得PM⊥BC ,由线面垂直判定定理得BC⊥平面PMB,最后根据面面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解平面PMC法向量,根据向量数量积求向量夹角,最后根据线面角与向量夹角互余关系求直线BN与平面PMC所成角的正弦值.
试题解析: (1)证明 ∵四边形ABCD是菱形,∠ADC=120°,
且M是AD的中点,∴MB⊥AD,∴MB⊥BC.
又∵P在底面ABCD的射影M是AD的中点,
∴PM⊥平面ABCD,
又∵BC平面ABCD,∴PM⊥BC,
而PM∩MB=M,PM,MB平面PMB,
∴BC⊥平面PMB,又BC平面PBC,
∴平面MPB⊥平面PBC.
(2)解 法一 过点B作BH⊥MC,连接HN,
∵PM⊥平面ABCD,BH平面ABCD,∴BH⊥PM,
又∵PM,MC平面PMC,PM∩MC=M,
∴BH⊥平面PMC,
∴HN为直线BN在平面PMC上的射影,
∴∠BNH为直线BN与平面PMC所成的角,
在菱形ABCD中,设AB=2a,则MB=AB·sin 60°=![]() a,
a,
MC=![]() =
=![]() a.
a.
又由(1)知MB⊥BC,
∴在△MBC中,BH=![]() =
=![]() a,
a,
由(1)知BC⊥平面PMB,PB平面PMB,
∴PB⊥BC,∴BN=![]() PC=
PC=![]() a,
a,
∴sin∠BNH=![]() =
=![]() =
=![]() .
.
法二 由(1)知MA,MB,MP两两互相垂直,以M为坐标原点,以MA,MB,MP所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系M-xyz,不妨设MA=1,
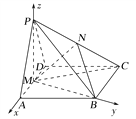
则M(0,0,0),A(1,0,0),B(0,![]() ,0),P(0,0,
,0),P(0,0,![]() ,0),
,0),
∵N是PC的中点,∴N![]() ,
,
设平面PMC的法向量为n=(x0,y0,z0),
又∵![]() =(0,0,
=(0,0,![]() ),
),![]() =(-2,
=(-2,![]() ,0),
,0),
∴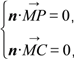 即
即![]()
令y0=1,则n=![]() ,|n|=
,|n|=![]() ,
,
又∵![]() =
=![]() ,|
,|![]() |=
|=![]() ,
,
|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() .
.
所以,直线BN与平面PMC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区的区人大代表有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为![]() ,乙校教师记为
,乙校教师记为![]() ,丙校教师记为
,丙校教师记为![]() ,丁校教师记为
,丁校教师记为![]() .现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.
(1)请列出十九大报告宣讲团组成人员的全部可能结果;
(2)求教师![]() 被选中的概率;
被选中的概率;
(3)求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆的一个顶点与两个焦点构成的三角形面积为2.
,椭圆的一个顶点与两个焦点构成的三角形面积为2.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与
两点,且与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(i)若![]() ,求
,求![]() 的值;
的值;
(ii)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-4,4]上的奇函数,当x∈(0,4]时,函数的解析式为![]() (a∈R), 且
(a∈R), 且![]() .
.
(1)试求a的值;
(2)求f(x)在[-4,4]上的解析式;
(3)求f(x)在[-4,0)上的最值(最大值和最小值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 部分图象如图所示.
部分图象如图所示.
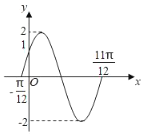
(1)求函数![]() 的解析式及
的解析式及![]() 的单调递增区间;
的单调递增区间;
(2)把函数![]() 图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图象上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 上所有的实数根之和.
上所有的实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com