试题分析:由于a,b小于0,所以只需研究x<0的函数的性质,利用绝对值的意义去掉绝对值符号,得到分段函数;当x<0时,
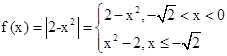
,然后结合二次函数的 心智可知
∴f(x)在(-∞,-
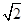
)递减;在(-
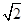
,0)递增
∵a<b<0,且f(a)=f(b),代入解析式得到a,b的范围
∴a≤-
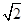
,0>b>-
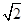
且a
2-2="-" a
2+2,解得a=-
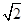
;-
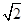
<b<0,∴0<ab<2
点评:解决该试题的关键是根据a,b小于0,所以只需研究x<0的函数的性质,利用绝对值的意义去掉绝对值符号,得到分段函数;得到f(x)在x<0上的单调性;判断出a,b的范围,利用f(a)=f(b),列出方程求出a的值,求出ab的范围.

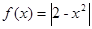 ,若
,若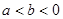 ,且
,且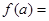
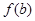 ,则
,则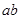 的取值范围是
的取值范围是