
设 ,其中
,其中 为正整数.
为正整数.
(1)求 ,
, ,
, 的值;
的值;
(2)猜想满足不等式 的正整数
的正整数 的范围,并用数学归纳法证明你的猜想.
的范围,并用数学归纳法证明你的猜想.
(1)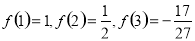 ;(2)
;(2)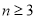
【解析】
试题分析:(1)数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题;(2)用数学归纳法证明等式问题,要“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始值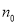 是多少;(3)由
是多少;(3)由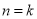 时等式成立,推出
时等式成立,推出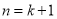 时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
试题解析:【解析】
(1)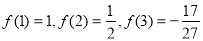 3分
3分
(2)猜想: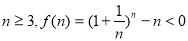 4分
4分
证明:①当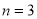 时,
时, 成立 5分
成立 5分
②假设当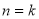
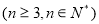 时猜想正确,即
时猜想正确,即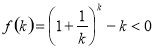
∴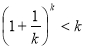
由于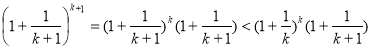
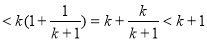 8分
8分
∴ ,即
,即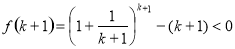 成立
成立
由①②可知,对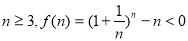 成立 10分
成立 10分
考点:数学归纳法及其应用.


科目:高中数学 来源:2015届山东省文登市高二下学期期末理科数学试卷(解析版) 题型:选择题
在吸烟与患肺病这两个事件的统计计算中,下列说法正确的是
A.若 的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;
C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误;
D.以上三种说法都不正确.
查看答案和解析>>
科目:高中数学 来源:2015届山东省文登市高二下学期期末理科数学试卷(解析版) 题型:选择题
在某项测量中,测量结果 服从正态分布
服从正态分布 ,若
,若 在
在 内取值的概率为
内取值的概率为 ,则
,则 在
在 内取值的概率为
内取值的概率为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省威海市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
曲线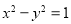 经过伸缩变换T得到曲线
经过伸缩变换T得到曲线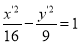 ,那么直线
,那么直线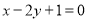 经过伸缩变换T得到的直线方程为( )
经过伸缩变换T得到的直线方程为( )
A.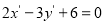 B.
B.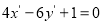
C.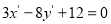 D.
D.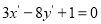
查看答案和解析>>
科目:高中数学 来源:2015届山东省乳山市高二下学期中考试理科数学试卷(解析版) 题型:选择题
定义:若存在常数 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,均有
,均有 成立,则称函数
成立,则称函数 在定义域
在定义域 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为( )
的最小值为( )
A.4 B.3 C.1 D.
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁鱼台二中高二3月质量检测理科数学试卷(解析版) 题型:选择题
已知 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .若
.若 ,其中
,其中 为常数,则动点
为常数,则动点 的轨迹不可能是( )
的轨迹不可能是( )
A.圆 B.椭圆 C.抛物线 D.双曲线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com