
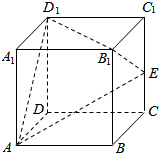
 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{23}{24}$ |
分析 分别取B1B、B1C1的中点M、N,连接AM、MN、AN,证明平面A1MN∥平面D1AE,可得点F的轨迹是线段MN,即可求出剩余几何体的体积.
解答  解:分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
解:分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,∴A1M∥平面D1AE.
同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线,∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F的轨迹是线段MN,
∴${V}_{{B}_{1}-AMN}$=$\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{24}$,
∴将B1点所在的几何体削去,剩余几何体的体积为1-$\frac{1}{24}$=$\frac{23}{24}$,
故选:D.
点评 本题考查了空间直线与平面平行关系的判定与性质,考查棱锥的体积公式,综合性较强,正确的作出图形是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
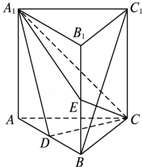 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=2,$A{A_1}=AC=BC=\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com