
分析 将f(x)写成分段函数的形式,求得f(x)的对称轴为x=$\frac{m-1}{2}$,代入即可得到最小值,解方程可得m的值.
解答 解:函数f(x)=max{|x+1|,|x-m|}
=$\left\{\begin{array}{l}{|x+1|,|x+1|≥|x-m|}\\{|x-m|,|x+1|<|x-m|}\end{array}\right.$,
由f(x)的解析式可得,f($\frac{m-1}{2}$+x)=f($\frac{m-1}{2}$-x),
即有f(x)的对称轴为x=$\frac{m-1}{2}$,
则f($\frac{m-1}{2}$)=|$\frac{m+1}{2}$|=$\frac{3}{2}$,
解得m=2或-4,
故答案为:2或-4.
点评 本题考查新定义的理解和运用,考查绝对值函数的最值的求法,运用对称性是解题的关键,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )
如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF是正三角形,EF∥AB,EF=2,则该多面体的体积为( )| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
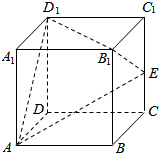 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{23}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | 2n+1 | C. | n2-1 | D. | 2n-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com