
分析 根据圆的性质,得直线x+my-1=0与直线y=x垂直且圆心C,在直线y=x上,由此解出m、n,从而得到直线和圆的方程,再由圆心C到直线的距离小于半径,利用点到直线的距离公式即可算出实数p的取值范围.
解答 解:根据题意,由于直线x+my-1=与圆C:x2+y2+mx+ny+4p=O交于 A,B两点,且A,B两点关于直线y=x对称,
则可知直线AB的斜率为-1,故可知m=1,
∴圆心C(-$\frac{m}{2}$,-$\frac{n}{2}$)在直线y=x上,可得m=n=1.
并且AB中点坐标在y=x上,联立方程$\left\{\begin{array}{l}y=x\\ x+y-1=0\end{array}\right.$,得到交点横坐标为x=$\frac{1}{2}$,则y=$\frac{1}{2}$,
则该点($\frac{1}{2}$,$\frac{1}{2}$)在圆内部,圆C:x2+y2+x+y+4p=0,圆心C(-$\frac{1}{2}$,-$\frac{1}{2}$),半径R=$\sqrt{1+1-16p}$=$\sqrt{2-16p}$,
∵直线x+y-1=0与圆C相交,
∴$\frac{|-\frac{1}{2}-\frac{1}{2}-1|}{\sqrt{2}}<\sqrt{2-16p}$,解之得p<0,
则实数P的取值范围为(-∞,0).
故答案为:(-∞,0).
点评 此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,垂径定理,勾股定理,以及点到直线的距离公式,当直线与圆相交时,常常根据垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
若某人在点 测得金字塔顶端仰角为
测得金字塔顶端仰角为 ,此人往金字塔方向走了80米到达点
,此人往金字塔方向走了80米到达点 ,测得金字塔顶端的仰角为
,测得金字塔顶端的仰角为 ,则金字塔的高度最接近于(忽略人的身高)(参考数据
,则金字塔的高度最接近于(忽略人的身高)(参考数据 )( )
)( )
A.110米 B.112米
C.220米 D.224米
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
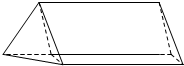 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y+1=0 | B. | x+2y+2=0 | C. | x-2y-2=0 | D. | 2x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com