Question

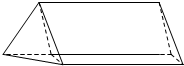
14．如图所示，放置在水平上的组合体由直三棱柱ABC-A₁B₁C₁与正三棱柱B-ABCD组成（D在B₁B的延长线上），它的正视图，俯视图，侧视图的面积分别为$2\sqrt{2}+1，2\sqrt{2}+1，1$．
（Ⅰ） 求证：AB⊥BC₁；
（Ⅱ） 求直线CA₁与平面ACD所成角的正弦值；
（Ⅲ） 在线段AC₁上是否存在点P，使B₁P⊥平面ACD，若存在，确定点P的位置；若不存在，说明理由．

Answer 1

分析 （Ⅰ） 根据正视图、俯视图、从左向右的侧视图的面积分别为$2\sqrt{2}+1，2\sqrt{2}+1，1$，从而可确定BA，BB₁的长．以点B为原点，分别以BC、BB₁、BA为x轴、y轴、z轴建立空间直角坐标系，求得$\overrightarrow{AB}$，$\overrightarrow{B{C}_{1}}$的坐标，由$\overrightarrow{AB}$•$\overrightarrow{B{C}_{1}}$=0，可得AB⊥BC₁；
（Ⅱ）求出平面ACD的法向量，进而可利用夹角公式求出直线CA₁与平面ACD所成角的正弦；
（Ⅲ）假设存在$\overrightarrow{AP}$=m$\overrightarrow{A{C}_{1}}$=（$\sqrt{2}m$，2m，-$\sqrt{2}m$），利用$\overrightarrow{{B}_{1}P}$与平面ACD的法向量，得方程即可求解．

解答 解：（Ⅰ）设BA=BC=BD=a，BB₁=b，由条件$\left\{\begin{array}{l}{ab+\frac{1}{2}{a}^{2}=2\sqrt{2}+1}\\{\frac{1}{2}{a}^{2}=1}\end{array}\right.$，可得$\left\{\begin{array}{l}{a=\sqrt{2}}\\{b=2}\end{array}\right.$．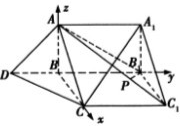
以点B为原点，分别以BC、BB₁、BA为x轴、y轴、z轴建立空间直角坐标系，则：A（0，0，$\sqrt{2}$），C（$\sqrt{2}$，0，0），D（0，-$\sqrt{2}$，0），
B1（0，2，0），C1（$\sqrt{2}$，2，0），A1（0，2，$\sqrt{2}$），（5分）
∴$\overrightarrow{AB}$=（0，0，-$\sqrt{2}$），$\overrightarrow{B{C}_{1}}$=（$\sqrt{2}$，2，0），
∴由$\overrightarrow{AB}$•$\overrightarrow{B{C}_{1}}$=0，可得AB⊥BC₁；
（Ⅱ）∵△ACD的重心G（$\frac{\sqrt{2}}{3}$，-$\frac{\sqrt{2}}{3}$，$\frac{\sqrt{2}}{3}$），∴$\overrightarrow{a}$=$\overrightarrow{BG}$=（$\frac{\sqrt{3}}{2}$，-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$）为平面ACD的法向量．（7分）
又$\overrightarrow{C{A}_{1}}$=（-$\sqrt{2}$，2，$\sqrt{2}$），则cos＜$\overrightarrow{a}$，$\overrightarrow{C{A}_{1}}$＞=$\frac{-\frac{2\sqrt{2}}{3}}{2\sqrt{2}×\frac{\sqrt{6}}{3}}$=$\frac{\sqrt{6}}{6}$．（9分）
∴所求角的正弦值为$\frac{\sqrt{6}}{6}$．（10分）
（Ⅲ）令$\overrightarrow{AP}$=m$\overrightarrow{A{C}_{1}}$=（$\sqrt{2}$m，2m，-$\sqrt{2}$m），（11分）
∴$\overrightarrow{{B}_{1}P}=\overrightarrow{{B}_{1}A}+\overrightarrow{AP}$=（$\sqrt{2}m$，2m-2，$\sqrt{2}-\sqrt{2}m$）=$λ\overrightarrow{a}$．
∴$\left\{\begin{array}{l}{\stackrel{\sqrt{2}m=\frac{\sqrt{2}λ}{3}}{2m-2=-\frac{\sqrt{2}λ}{3}}}\\{\sqrt{2}-\sqrt{2}m=\frac{\sqrt{2}λ}{3}}\end{array}\right.$，可得无解．
∴不存在满足条件的点P．

点评 本题以组合体为载体，主要考查了直线与平面垂直的判定，线面角，空间中直线与直线之间的位置关系，考查了空间想象能力和推理论证能力，解题的关键是构建空间直角坐标系，属于中档题．