
分析 由已知中f(x)=sin(ωx+$\frac{π}{6}$)的图象关于直线x=$\frac{π}{6}$对称,故当x=$\frac{π}{6}$时,f(x)取最大值,或最小值,(ω+1)$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,进而得到答案.
解答 解:∵f(x)=sin(ωx+$\frac{π}{6}$)的图象关于直线x=$\frac{π}{6}$对称,
故当x=$\frac{π}{6}$时,f(x)取最大值,或最小值,
即(ω+1)$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
即ω=6k+2,k∈Z,
故答案为:6k+2,k∈Z,
点评 本题考查的知识点是正弦型函数的图象和性质,熟练掌握正弦型函数的图象和性质,是解答的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:2017届广西陆川县中学高三9月月考数学(文)试卷(解析版) 题型:选择题
如图,边长为 的等边三角形
的等边三角形 的中线
的中线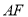 与中位线
与中位线 交于点
交于点 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形,则下列命题中正确的是( )
旋转过程中的一个图形,则下列命题中正确的是( )

① ;②
;② 平面
平面 ;③三棱锥
;③三棱锥 的体积有最大值.
的体积有最大值.
A.① B.①② C.①②③ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
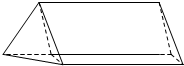 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y+1=0 | B. | x+2y+2=0 | C. | x-2y-2=0 | D. | 2x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com