
分析 通过讨论a=0和a≠0两种情况,从而综合得到结论.
解答 解:①a=0时,f(x)=3x-4,令f(x)=0,显然x=$\frac{4}{3}$在(0,2)内,成立;
②a≠0时,f(x)=3ax2+(3-4a)x-4=(3x-4)(ax+1),
令f(x)=0,得:x=$\frac{4}{3}$,或x=-$\frac{1}{a}$,
∴只需0<-$\frac{1}{a}$<2即可,解得:a<-$\frac{1}{2}$,
综上:a的范围是:$(-∞\;,\;\;-\frac{1}{2})∪\{0\}$,
故答案为:(-∞,-$\frac{1}{2}$)∪{0}.
点评 本题考查了函数的零点问题,考查二次函数的性质,是一道基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:解答题
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, .
.
(1)当 ,
, ,
, 成等差数列时,求
成等差数列时,求 的面积;
的面积;
(2)设 为
为 边的中点,求线段
边的中点,求线段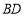 长的最小值.
长的最小值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
已知等差数列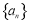 中,
中, ,
, ,则
,则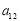 的值是( )
的值是( )
A.15 B.30 C.31 D.64
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.
如图所示,点E为矩形ABCD边CD的中点,AB=2,AD=$\sqrt{2}$,将△ADE沿AE折起到△AD1E的位置,使得平面AD1E⊥平面ABCE,连接BD1、CD1,得到如图乙所示的几何体.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com