
分析 (1)由题意和两角和的正切公式求出tan(A+B)的值,由内角的范围求出A+B,由内角和定理求出角C的值;
(2)由正切函数值判断出最大边、最小边,根据同角三角函数的基本关系求出sinB的值,由正弦定理求出最短边的长.
解答 解:(1)由题意知,tanA=$\frac{1}{2}$,tanB=$\frac{1}{3}$,
则tan(A+B)=$\frac{tanA+tanB}{1-tanAtanB}$=$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=1,
∵0<A+B<π,∴A+B=$\frac{π}{4}$,
∴∠C=π-(A+B)=$π-\frac{π}{4}$=$\frac{3π}{4}$;
(2)∴tanA=$\frac{1}{2}$>tanB=$\frac{1}{3}$,∴B是最小角,b是最小边,
由(1)知,∠C=$\frac{3π}{4}$是最大角,则c是最大边,c=$5\sqrt{5}$,
由$\left\{\begin{array}{l}{tanB=\frac{sinB}{cosB}=\frac{1}{3}}\\{si{n}^{2}B+co{s}^{2}B=1}\end{array}\right.$得,sin2B=$\frac{1}{10}$,
又B是最小角,则sinB=$\frac{\sqrt{10}}{10}$,
由正弦定理得$\frac{b}{sinB}=\frac{c}{sinC}$,∴b=$\frac{csinB}{sinC}$=$\frac{5\sqrt{5}×\frac{\sqrt{10}}{10}}{\frac{\sqrt{2}}{2}}$=5,
则最短边的长是5.
点评 本题考查正弦定理,两角和的正切公式,边角关系,注意内角的范围,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
已知数列:2,0,2,0,2,0……前六项不适合下列哪个通项公式( )
A.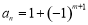 B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
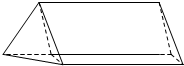 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com