
分析 分别求出命题p,q为真时,a的取值范围,
(1)若p且q为真命题,则两个取值范围的交集即为答案;
(2)若p或q为真命题,则两个取值范围的并集即为答案;
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,x<0}\\{ln(x+1),x≥0}\end{array}\right.$,
∴y=|f(x)|=$\left\{\begin{array}{l}{x}^{2}-2x,x<0\\ ln(x+1),x≥0\end{array}\right.$,
∴y′=$\left\{\begin{array}{l}2x-2,x<0\\ \frac{1}{x+1},x≥0\end{array}\right.$,
由y=|f(x)|和y=ax的图象均过原点,
故命题p为真,即|f(x)|≥ax恒成立时,
仅须y′|x=0=-2≤a≤0,
即a∈[-2,0],
∵当x≥0时,f(x)=$\frac{1}{2}$(|x-a2|+|x-2a2|-3a2).
∴当0≤x≤a2时,f(x)=$\frac{1}{2}$(a2-x+2a2-x-3a2)=-x;
当a2<x≤2a2时,f(x)=-a2;
当x>2a2时,f(x)=x-3a2.
画出其图象.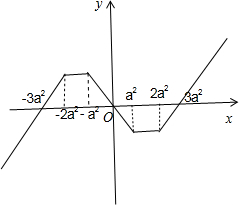
由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,
与x>0时的图象关于原点对称.
若命题q为真,即?x∈R,f(x-1)≤f(x),
即6a2≤1,
解得:a∈[-$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{6}}{6}$].
(1)若p且q为真命题,则a∈[-$\frac{\sqrt{6}}{6}$,0];
(2)若p或q为真命题,则∈[-2,$\frac{\sqrt{6}}{6}$].
点评 本题考查的知识点是命题的真假判断与应用,复合命题的真假,恒成立问题,难度较大,属于难题.


科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,30) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻井深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 短轴长 | B. | 长轴长 | C. | 离心率 | D. | 对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com