练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线的离心率为2，过点、斜率为1的直线与双曲线交于、两点且，.

    （1）求双曲线方程。

    （2）设为双曲线右支上动点，为双曲线的右焦点，在轴负半轴上是否存在定点，使得？若存在，求出点的坐标；若不存在，请说明理由。

    【答案】（1）；（2）见解析

    【解析】

    （1）由双曲线离心率为2知，.

    于是，双曲线方程可化为.

    又直线，与双曲线方程联立得

    ①

    设点，.则

    ，. ②

    因为，所以，

    .故.

    结合，解得，.

    代入式②得

    又

    ，

    从而，.

    此时，，代入式①并整理得

    .

    显然，该方程有两个不同的实根.

    因此，符合要求.故双曲线的方程为

    （2）假设点存在.由（1）知双曲线右焦点为.

    设为双曲线右支上一点.

    当时，，.

    因为，所以，.

    将代入上式并整理得

    .

    当时，，而时，，符合.

    所以，满足条件的点存在.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】西北某省会城市计划新修一座城市运动公园，设计平面如图所示：其为五边形，其中三角形区域为球类活动场所；四边形为文艺活动场所，，为运动小道（不考虑宽度），，千米.

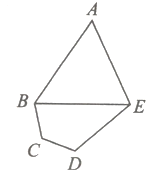
    （1）求小道的长度；

    （2）求球类活动场所的面积最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）判断函数的奇偶性，并说明理由；

    （2）若在上的最小值为3，求实数的值以及相应的的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若，求证：

    （2）若，恒有，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．

    (1)求M∩P＝{x|5<x≤8}的充要条件；

    (2)求实数a的一个值，使它成为M∩P＝{x|5<x≤8}的一个充分但不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数=Asin（A>0，>0，<≤）在处取得最大值2，其图象与x轴的相邻两个交点的距离为。

    （1）求的解析式；

    （2）求函数 的值域。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100名顾客的相关数据，如下表所示：

    已知这100位顾客中一次性购物超过8件的顾客占55%.

    一次性购物

    1至4件

    5至8件

    9至12件

    13至16件

    17件及以上

    顾客数（人）

    30

    25

    10

    结算时间（分/人）

    1

    1.5

    2

    2.5

    3

    （1）求，的值；

    （2）求一位顾客一次购物的结算时间超过2分钟的概率（频率代替概率）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为,且.

    (1)求数列的通项公式；

    (2)设数列的前项和为，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某投资公司在年年初准备将万元投资到“低碳”项目上，现有两个项目供选择：

    项目一：新能源汽车.据市场调研，投资到该项目上，到年底可能获利，也可能亏损，且这两种情况发生的概率分别为和；

    项目二：通信设备.据市场调研，投资到该项目上，到年底可能获利，可能损失，也可能不赔不赚，且这三种情况发生的概率分别为、和.

    针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由.

    查看答案和解析>>

    同步练习册答案