
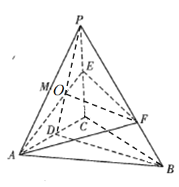
【题目】如图,在三棱锥PABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分别是AC,PC的中点,F是PB上一点,且
,D,E分别是AC,PC的中点,F是PB上一点,且![]() ,M为PA的中点,二面角
,M为PA的中点,二面角![]() 的大小为45°.
的大小为45°.

(1)证明:![]() 平面AEF;
平面AEF;
(2)求直线AF与平面BCM所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接PD交AE于点O,因为D,E分别是AC,PC的中点,则点O是![]() 的重心,所以
的重心,所以![]() ,连接OF,又
,连接OF,又![]() ,所以
,所以![]() ,从而可证明结论.
,从而可证明结论.
(2)由题意可证得![]() 即二面角
即二面角![]() 的平面角,即
的平面角,即![]() ,可得
,可得![]() ,则
,则![]() ,得到
,得到![]() ,又由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系
,又由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系![]() ,用向量法求解线面角.
,用向量法求解线面角.
解:(1)连接PD交AE于点O,因为D,E分别是AC,PC的中点,
所以点O是![]() 的重心,所以
的重心,所以![]() .
.
连接OF,又![]() ,所以
,所以![]() ,则
,则![]() .
.
又![]() 平面AEF,
平面AEF,![]() 平面AEF,所以
平面AEF,所以![]() 平面AEF.
平面AEF.
(2)因为![]() 底面ABC,
底面ABC,![]() 平面ABC,所以
平面ABC,所以![]() .又
.又![]() ,
,![]() ,
,
所以![]() 平面PAC.所以
平面PAC.所以![]() ,又
,又![]() ,所以
,所以![]() 即二面角
即二面角![]() 的平面角,
的平面角,
所以![]() ,连接MD,易得
,连接MD,易得![]() ,则
,则![]() ,所以
,所以![]() .
.
由题意易知,CA,CB,CP两两垂直,故以C为坐标原点,直线CA,CB,CP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,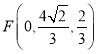 ,
,
所以![]() ,
,![]() ,
,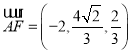 .
.
设平面BCM的法向量为![]() ,则
,则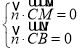 ,得
,得 ,得
,得![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() 为平面BCM的一个法向量.
为平面BCM的一个法向量.
设直线AF与平面BCM所成的角为![]() .
.
则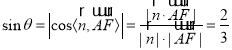
故直线AF与平面BCM所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处取得极大值或极小值,则称
处取得极大值或极小值,则称![]() 为函数
为函数![]() 的极值点.设函数
的极值点.设函数![]() .
.
(1)若函数![]() 在
在![]() 上无极值点,求
上无极值点,求![]() 的取值范围;
的取值范围;
(2)求证:对任意实数![]() ,在函数
,在函数![]() 的图象上总存在两条切线相互平行;
的图象上总存在两条切线相互平行;
(3)当![]() 时,若函数
时,若函数![]() 的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
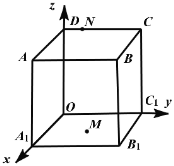
【题目】单位正方体![]() 在空间直角坐标系中的位置如图所示,动点
在空间直角坐标系中的位置如图所示,动点![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,设由
,设由![]() ,
,![]() ,
,![]() 三点确定的平面截该正方体的截面为
三点确定的平面截该正方体的截面为![]() ,那么( )
,那么( )
A.对任意点![]() ,存在点
,存在点![]() 使截面
使截面![]() 为三角形
为三角形
B.对任意点![]() ,存在点
,存在点![]() 使截面
使截面![]() 为正方形
为正方形
C.对任意点![]() 和
和![]() ,截面
,截面![]() 都为梯形
都为梯形
D.对任意点![]() ,存在点
,存在点![]() 使得截面
使得截面![]() 为矩形
为矩形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研,随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析,将结果列成频率分布表如下:
数学成绩 | 频数 | 频率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合计 | 200 | 1 |
根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级,其中成绩大于或等于80分的为“优秀”,成绩小于60分的为“不合格”,其余的成绩为“合格”.
(1)根据频率分布表中的数据,估计全市学业水平考试的数学成绩的众数、中位数(精确到0.1);
(2)市数学教研员从样本中又随机选取了![]() 名高中生的学业水平考试的数学成绩,如果这
名高中生的学业水平考试的数学成绩,如果这![]() 的最小值;
的最小值;
(3)估计全市2018级高中生学业水平考试“不合格”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂质检部门要对该厂流水线生产出的一批产品进行检验,如果检查到第![]() 件仍未发现不合格品,则此次检查通过且认为这批产品合格,如果在尚未抽到第
件仍未发现不合格品,则此次检查通过且认为这批产品合格,如果在尚未抽到第![]() 件时已检查到不合格品则拒绝通过且认为这批产品不合格.设这批产品的数量足够大,可以认为每次检查查到不合格品的概率都为
件时已检查到不合格品则拒绝通过且认为这批产品不合格.设这批产品的数量足够大,可以认为每次检查查到不合格品的概率都为![]() ,即每次抽查的产品是相互独立的.
,即每次抽查的产品是相互独立的.
(1)若![]() ,求这批产品能够通过检查的概率;
,求这批产品能够通过检查的概率;
(2)已知每件产品质检费用为50元,若![]() ,设对这批产品的质检个数记作
,设对这批产品的质检个数记作![]() ,求
,求![]() 的分布列;
的分布列;
(3)在(2)的条件下,已知1000批此类产品,若![]() ,则总平均检查费用至少需要多少元?(总平均检查费用
,则总平均检查费用至少需要多少元?(总平均检查费用![]() 每批次平均检查费用
每批次平均检查费用![]() 批数)
批数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,某十字路口的花圃中央有一个底面半径为
,某十字路口的花圃中央有一个底面半径为![]() 的圆柱形花柱,四周斑马线的内侧连线构成边长为
的圆柱形花柱,四周斑马线的内侧连线构成边长为![]() 的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器
的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器![]() 的移动速度为
的移动速度为![]() ,仪器
,仪器![]() 的移动速度为
的移动速度为![]() .若仪器
.若仪器![]() 与仪器
与仪器![]() 的对视光线被花柱阻挡,则称仪器
的对视光线被花柱阻挡,则称仪器![]() 在仪器
在仪器![]() 的“盲区”中.
的“盲区”中.



(1)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 在点
在点![]() 处,仪器
处,仪器![]() 在
在![]() 上距离点
上距离点![]()
![]() 处,试判断仪器
处,试判断仪器![]() 是否在仪器
是否在仪器![]() 的“盲区”中,并说明理由;
的“盲区”中,并说明理由;
(2)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,同时仪器
移动,同时仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,在这个移动过程中,仪器
移动,在这个移动过程中,仪器![]() 在仪器
在仪器![]() 的“盲区”中的时长为多少?
的“盲区”中的时长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 、
、![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 、
、![]() 互相垂直.点M在
互相垂直.点M在![]() 上移动,点N在
上移动,点N在![]() 上移动,若
上移动,若![]() (
(![]() ).
).

(1)当a为何值时,![]() 的长最小;
的长最小;
(2)当![]() 长最小时,求面
长最小时,求面![]() 与面
与面![]() 所成的二面角α的余弦值.
所成的二面角α的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com