
°ĺŐ‚ńŅ°Ņ»ÁÕľ![]() £¨ń≥ ģ◊÷¬∑ŅŕĶńĽ®∆‘÷–—Ž”–“ĽłŲĶ◊√śįŽĺ∂ő™
£¨ń≥ ģ◊÷¬∑ŅŕĶńĽ®∆‘÷–—Ž”–“ĽłŲĶ◊√śįŽĺ∂ő™![]() Ķń‘≤÷ý–őĽ®÷ý£¨ňń÷‹įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…ĪŖ≥§ő™
Ķń‘≤÷ý–őĽ®÷ý£¨ňń÷‹įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…ĪŖ≥§ő™![]() Ķń’ż∑Ĺ–ő.“ÚĻ§≥Ő–Ť“™£¨≤‚ŃŅ‘ĪĹę Ļ”√“«∆ų—ōįŖ¬ŪŌŖĶńńŕ≤ŗĹÝ––≤‚ŃŅ£¨∆š÷–“«∆ų
Ķń’ż∑Ĺ–ő.“ÚĻ§≥Ő–Ť“™£¨≤‚ŃŅ‘ĪĹę Ļ”√“«∆ų—ōįŖ¬ŪŌŖĶńńŕ≤ŗĹÝ––≤‚ŃŅ£¨∆š÷–“«∆ų![]() Ķń“∆∂ĮňŔ∂»ő™
Ķń“∆∂ĮňŔ∂»ő™![]() £¨“«∆ų
£¨“«∆ų![]() Ķń“∆∂ĮňŔ∂»ő™
Ķń“∆∂ĮňŔ∂»ő™![]() .»Ű“«∆ų
.»Ű“«∆ų![]() ”Ž“«∆ų
”Ž“«∆ų![]() Ķń∂‘ ”Ļ‚ŌŖĪĽĽ®÷ý◊ŤĶ≤£¨‘Ú≥∆“«∆ų
Ķń∂‘ ”Ļ‚ŌŖĪĽĽ®÷ý◊ŤĶ≤£¨‘Ú≥∆“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–.
Ķń°į√§«Ý°Ī÷–.



£®1£©»ÁÕľ![]() £¨įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…’ż∑Ĺ–ő
£¨įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…’ż∑Ĺ–ő![]() £¨“«∆ų
£¨“«∆ų![]() ‘ŕĶ„
‘ŕĶ„![]() ī¶£¨“«∆ų
ī¶£¨“«∆ų![]() ‘ŕ
‘ŕ![]() …ŌĺŗņŽĶ„
…ŌĺŗņŽĶ„![]()
![]() ī¶£¨ ‘Ň–∂Ō“«∆ų
ī¶£¨ ‘Ň–∂Ō“«∆ų![]() «∑Ů‘ŕ“«∆ų
«∑Ů‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–£¨≤ĘňĶ√ųņŪ”…£Ľ
Ķń°į√§«Ý°Ī÷–£¨≤ĘňĶ√ųņŪ”…£Ľ
£®2£©»ÁÕľ![]() £¨įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…’ż∑Ĺ–ő
£¨įŖ¬ŪŌŖĶńńŕ≤ŗѨŌŖĻĻ≥…’ż∑Ĺ–ő![]() £¨“«∆ų
£¨“«∆ų![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑ĘŌÚĶ„
≥Ų∑ĘŌÚĶ„![]() “∆∂Į£¨Õ¨ Ī“«∆ų
“∆∂Į£¨Õ¨ Ī“«∆ų![]() ī”Ķ„
ī”Ķ„![]() ≥Ų∑ĘŌÚĶ„
≥Ų∑ĘŌÚĶ„![]() “∆∂Į£¨‘ŕ’‚łŲ“∆∂ĮĻż≥Ő÷–£¨“«∆ų
“∆∂Į£¨‘ŕ’‚łŲ“∆∂ĮĻż≥Ő÷–£¨“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™∂ŗ…Ŕ£Ņ
Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™∂ŗ…Ŕ£Ņ
°ĺīūįł°Ņ£®1£© «£¨ņŪ”…ľŻĹ‚őŲ£Ľ£®2£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨«ůĶ√Ķ„![]() °Ę
°Ę![]() Ķń◊ÝĪÍ£¨ĹÝ∂ÝŅ…Ķ√≥Ų÷ĪŌŖ
Ķń◊ÝĪÍ£¨ĹÝ∂ÝŅ…Ķ√≥Ų÷ĪŌŖ![]() Ķń∑Ĺ≥Ő£¨«ů≥Ų‘≠Ķ„
Ķń∑Ĺ≥Ő£¨«ů≥Ų‘≠Ķ„![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ£¨Ň–∂Ō÷ĪŌŖ
ĶńĺŗņŽ£¨Ň–∂Ō÷ĪŌŖ![]() ”ŽĽ®÷ýňý‘ŕ‘≤ĶńőĽ÷√ĻōŌĶ£¨”…īňŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
”ŽĽ®÷ýňý‘ŕ‘≤ĶńőĽ÷√ĻōŌĶ£¨”…īňŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
£®2£©Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨«ů≥Ų![]() °Ę
°Ę![]() °Ę
°Ę![]() °Ę
°Ę![]() Ķń◊ÝĪÍ£¨ľŔ…Ť“«∆ų
Ķń◊ÝĪÍ£¨ľŔ…Ť“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™
Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™![]() £¨”√
£¨”√![]() ĪŪ ĺĶ„
ĪŪ ĺĶ„![]() °Ę
°Ę![]() Ķń◊ÝĪÍ£¨≤Ę«ů≥Ų÷ĪŌŖ
Ķń◊ÝĪÍ£¨≤Ę«ů≥Ų÷ĪŌŖ![]() Ķń∑Ĺ≥Ő£¨ņŻ”√‘≤–ń
Ķń∑Ĺ≥Ő£¨ņŻ”√‘≤–ń![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ
ĶńĺŗņŽ![]() Ņ…Ķ√≥ŲĻō”ŕ
Ņ…Ķ√≥ŲĻō”ŕ![]() Ķń≤ĽĶ» Ĺ£¨«ů≥Ų
Ķń≤ĽĶ» Ĺ£¨«ů≥Ų![]() Ķń»°÷Ķ∑∂őߣ¨”…īňŅ…Ķ√≥ŲĹŠĻŻ.
Ķń»°÷Ķ∑∂őߣ¨”…īňŅ…Ķ√≥ŲĹŠĻŻ.
£®1£©Ĺ®ŃĘ»ÁÕľ![]() ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨‘Ú
ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨‘Ú![]() £¨
£¨![]() £¨ňý“‘
£¨ňý“‘![]() £¨
£¨
ňý“‘÷ĪŌŖ![]() Ķń∑Ĺ≥Ő «
Ķń∑Ĺ≥Ő «![]() £¨ľī
£¨ľī![]() £¨
£¨
Ļ ‘≤–ń![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ
ĶńĺŗņŽ![]() £¨
£¨
ňý“‘‘≤![]() ”Ž÷ĪŌŖ
”Ž÷ĪŌŖ![]() ŌŗĹĽ£¨Ļ “«∆ų
ŌŗĹĽ£¨Ļ “«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–£Ľ
Ķń°į√§«Ý°Ī÷–£Ľ
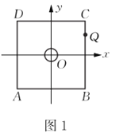
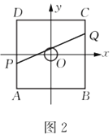
£®2£©Ĺ®ŃĘ»ÁÕľ![]() ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨
ňý ĺĶń∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ£¨
‘Ú![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
“ņŐ‚“‚÷™∆ū ľ ĪŅŐ“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–.
Ķń°į√§«Ý°Ī÷–.
ľŔ…Ť“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™
Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨![]() £¨
£¨
ňý“‘÷ĪŌŖ![]() Ķń–Ī¬
Ķń–Ī¬  £¨
£¨
Ļ ÷ĪŌŖ![]() Ķń∑Ĺ≥Ő «
Ķń∑Ĺ≥Ő «![]() £¨ľī
£¨ľī![]() £¨
£¨
ī”∂ÝĶ„![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ
ĶńĺŗņŽ £¨
£¨
’ŻņŪĶ√![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨ĹŠļŌ Īľš
£¨ĹŠļŌ Īľš![]() £¨Ķ√
£¨Ķ√![]() .
.
īū£ļ“«∆ų![]() ‘ŕ“«∆ų
‘ŕ“«∆ų![]() Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™
Ķń°į√§«Ý°Ī÷–Ķń Ī≥§ő™![]() .
.


 »ęń‹≤‚Ņō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
»ęń‹≤‚Ņō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨’ż∑ĹŐŚABCD©ĀA1B1C1D1Ķńņ‚≥§ő™a£¨ŌŖ∂őB1D1…Ō”–ŃĹłŲ∂ĮĶ„E£¨F£¨«“EF![]() a£¨“‘Ō¬ĹŠ¬Ř’ż»∑Ķń”–£®°°°°£©
a£¨“‘Ō¬ĹŠ¬Ř’ż»∑Ķń”–£®°°°°£©

A.AC°ÕBE
B.Ķ„AĶĹ°ųBEFĶńĺŗņŽő™∂®÷Ķ
C.»żņ‚◊∂A©ĀBEFĶńŐŚĽż «’ż∑ĹŐŚABCD©ĀA1B1C1D1ŐŚĽżĶń![]()
D.“ž√ś÷ĪŌŖAE£¨BFňý≥…ĶńĹ«ő™∂®÷Ķ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘໿ņ‚◊∂PABC÷–£¨![]() Ķ◊√śABC£¨
Ķ◊√śABC£¨![]() £¨
£¨![]() £¨
£¨![]() £¨D£¨E∑÷Īū «AC£¨PCĶń÷–Ķ„£¨F «PB…Ō“ĽĶ„£¨«“
£¨D£¨E∑÷Īū «AC£¨PCĶń÷–Ķ„£¨F «PB…Ō“ĽĶ„£¨«“![]() £¨Mő™PAĶń÷–Ķ„£¨∂Ģ√śĹ«
£¨Mő™PAĶń÷–Ķ„£¨∂Ģ√śĹ«![]() Ķńīů–°ő™45°„.
Ķńīů–°ő™45°„.

£®1£©÷§√ų£ļ![]() ∆Ĺ√śAEF£Ľ
∆Ĺ√śAEF£Ľ
£®2£©«ů÷ĪŌŖAF”Ž∆Ĺ√śBCMňý≥…Ĺ«Ķń’żŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥–£∂‘łŖ“ĽńÍľ∂—ß…ķļģľŔ≤őľ”…Á«Ý∑ĢőŮĶńīő żĹÝ––ŃňÕ≥ľ∆£¨ňśĽķ≥ť»°Ńň![]() √Ż—ß…ķ◊ųő™—ýĪĺ£¨Ķ√ĶĹ’‚
√Ż—ß…ķ◊ųő™—ýĪĺ£¨Ķ√ĶĹ’‚![]() √Ż—ß…ķ≤őľ”…Á«Ý∑ĢőŮĶńīő ż£¨łýĺ›īň żĺ›◊ų≥ŲŃň∆Ķ¬ ∑÷≤ľÕ≥ľ∆ĪŪļÕ∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁŌ¬£ļ
√Ż—ß…ķ≤őľ”…Á«Ý∑ĢőŮĶńīő ż£¨łýĺ›īň żĺ›◊ų≥ŲŃň∆Ķ¬ ∑÷≤ľÕ≥ľ∆ĪŪļÕ∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁŌ¬£ļ

£®1£©«ůĪŪ÷–![]() Ķń÷ĶļÕ∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷–
Ķń÷ĶļÕ∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ÷–![]() Ķń÷Ķ£¨≤Ęłýĺ›∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľĻņľ∆ł√–£łŖ“Ľ—ß…ķļģľŔ≤őľ”…Á«Ý∑ĢőŮīő żĶń÷–őĽ ż£Ľ
Ķń÷Ķ£¨≤Ęłýĺ›∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľĻņľ∆ł√–£łŖ“Ľ—ß…ķļģľŔ≤őľ”…Á«Ý∑ĢőŮīő żĶń÷–őĽ ż£Ľ
£®2£©»ÁĻŻ”√∑÷≤„≥ť—ýĶń∑Ĺ∑®ī”—ýĪĺ∑ĢőŮīő ż‘ŕ![]() ļÕ
ļÕ![]() Ķń»ň÷–Ļ≤≥ť»°6»ň£¨‘Ŕī”’‚6»ň÷–—°2»ň£¨«ů2»ň∑ĢőŮīő ż∂ľ‘ŕ
Ķń»ň÷–Ļ≤≥ť»°6»ň£¨‘Ŕī”’‚6»ň÷–—°2»ň£¨«ů2»ň∑ĢőŮīő ż∂ľ‘ŕ![]() ĶńłŇ¬ .
ĶńłŇ¬ .
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤C£ļ![]() £®
£®![]() £©ĶńņŽ–ń¬ ő™
£©ĶńņŽ–ń¬ ő™![]() £¨«“ĻżĶ„
£¨«“ĻżĶ„![]() .
.
£®1£©«ůÕ÷‘≤CĶń∑Ĺ≥Ő£Ľ
£®2£©Ļż◊ÝĪÍ‘≠Ķ„Ķń÷ĪŌŖ”ŽÕ÷‘≤ĹĽ”ŕM£¨NŃĹĶ„£¨ĻżĶ„M◊ų‘≤![]() Ķń“ĽŐű«–ŌŖ£¨ĹĽÕ÷‘≤”ŕŃŪ“ĽĶ„P£¨Ń¨Ĺ”
Ķń“ĽŐű«–ŌŖ£¨ĹĽÕ÷‘≤”ŕŃŪ“ĽĶ„P£¨Ń¨Ĺ”![]() £¨÷§√ų£ļ
£¨÷§√ų£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅňÔ◊”∂®ņŪ «÷–ĻķĻŇīķ«ůĹ‚“ĽīőÕ¨”ŗ Ĺ◊ťĶń∑Ĺ∑®£¨ « ż¬Ř÷–“ĽłŲ÷ō“™∂®ņŪ£¨◊Ó‘ÁŅ…ľŻ”ŕ÷–ĻķńŌĪĪ≥Į Ī∆ŕĶń ż—ß÷Ý◊ų°∂ňÔ◊”ň„ĺ≠°∑£¨![]() ńÍ”ĘĻķņīĽ™īęĹŐ ŅőįŃ“—«Ń¶Ĺę∆šő Ő‚ĶńĹ‚∑®īę÷ŃŇ∑÷ř£¨
ńÍ”ĘĻķņīĽ™īęĹŐ ŅőįŃ“—«Ń¶Ĺę∆šő Ő‚ĶńĹ‚∑®īę÷ŃŇ∑÷ř£¨![]() ńÍ”ĘĻķ ż—ßľ“¬Ūőų…≠÷ł≥Ųīň∑®∑ŻļŌ
ńÍ”ĘĻķ ż—ßľ“¬Ūőų…≠÷ł≥Ųīň∑®∑ŻļŌ![]() ńÍ”…łŖňĻĶ√≥ŲĶńĻō”ŕÕ¨”ŗ ĹĹ‚∑®Ķń“Ľį„–‘∂®ņŪ£¨“Ú∂Ýőų∑Ĺ≥∆÷ģő™°į÷–Ļķ £”ŗ∂®ņŪ°Ī£ģ’‚łŲ∂®ņŪĹ≤Ķń «“ĽłŲĻō”ŕ’Ż≥żĶńő Ő‚£¨Ō÷”–’‚—ý“ĽłŲ’Ż≥żő Ő‚£ļĹę
ńÍ”…łŖňĻĶ√≥ŲĶńĻō”ŕÕ¨”ŗ ĹĹ‚∑®Ķń“Ľį„–‘∂®ņŪ£¨“Ú∂Ýőų∑Ĺ≥∆÷ģő™°į÷–Ļķ £”ŗ∂®ņŪ°Ī£ģ’‚łŲ∂®ņŪĹ≤Ķń «“ĽłŲĻō”ŕ’Ż≥żĶńő Ő‚£¨Ō÷”–’‚—ý“ĽłŲ’Ż≥żő Ő‚£ļĹę![]() ÷Ń
÷Ń![]() ’‚
’‚![]() łŲ’Ż ż÷–ń‹ĪĽ
łŲ’Ż ż÷–ń‹ĪĽ![]() ≥ż”ŗ
≥ż”ŗ![]() «“ĪĽ
«“ĪĽ![]() ≥ż”ŗ
≥ż”ŗ![]() Ķń żįī”…–°ĶĹīůĶńň≥–ÚŇŇ≥…“ĽŃ–ĻĻ≥…“Ľ żŃ–£¨‘Úīň żŃ–ĶńŌÓ ż «£® £©
Ķń żįī”…–°ĶĹīůĶńň≥–ÚŇŇ≥…“ĽŃ–ĻĻ≥…“Ľ żŃ–£¨‘Úīň żŃ–ĶńŌÓ ż «£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™ŃňĹ‚»ę –Õ≥Ņľ«ťŅŲ£¨ī”ňý”–≤őľ”Ņľ ‘ĶńŅľ…ķ÷–≥ť»°4000√ŻŅľ…ķĶń≥…ľ®£¨∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁŌ¬Õľňý ĺ.

£®1£©«ů’‚4000√ŻŅľ…ķĶńįŽĺý≥…ľ®![]() £®Õ¨“Ľ◊ť÷– żĺ›”√ł√◊ť«Ýľš÷–Ķ„◊ųīķĪŪ£©£Ľ
£®Õ¨“Ľ◊ť÷– żĺ›”√ł√◊ť«Ýľš÷–Ķ„◊ųīķĪŪ£©£Ľ
£®2£©”…÷Ī∑ĹÕľŅ…»Ōő™Ņľ…ķŅľ ‘≥…ľ®z∑Ģī”’żŐ¨∑÷≤ľ![]() £¨∆š÷–
£¨∆š÷–![]() ∑÷Īū»°Ņľ…ķĶń∆Ĺĺý≥…ľ®
∑÷Īū»°Ņľ…ķĶń∆Ĺĺý≥…ľ®![]() ļÕŅľ…ķ≥…ľ®Ķń∑Ĺ≤Ó
ļÕŅľ…ķ≥…ľ®Ķń∑Ĺ≤Ó![]() £¨ń«√ī≥ť»°Ķń4000√ŻŅľ…ķ≥…ľ®≥¨Ļż84.81∑÷£®ļ¨84.81∑÷£©Ķń»ň żĻņľ∆”–∂ŗ…Ŕ»ň£Ņ
£¨ń«√ī≥ť»°Ķń4000√ŻŅľ…ķ≥…ľ®≥¨Ļż84.81∑÷£®ļ¨84.81∑÷£©Ķń»ň żĻņľ∆”–∂ŗ…Ŕ»ň£Ņ
£®3£©»ÁĻŻ”√≥ť»°ĶńŅľ…ķ≥…ľ®Ķń«ťŅŲņīĻņľ∆»ę –Ņľ…ķĶń≥…ľ®«ťŅŲ£¨Ō÷ī”»ę –Ņľ…ķ÷–ňśĽķ≥ť»°4√ŻŅľ…ķ£¨ľ«≥…ľ®≤Ľ≥¨Ļż84.81∑÷ĶńŅľ…ķ»ň żő™![]() £¨«ů
£¨«ů![]() .£®ĺę»∑ĶĹ0.001£©
.£®ĺę»∑ĶĹ0.001£©
łĹ£ļĘŔ![]() £Ľ
£Ľ
Ęŕ![]() £¨‘Ú
£¨‘Ú![]() £Ľ
£Ľ
ĘŘ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…ŤľĮļŌ![]() £¨…ŤľĮļŌ
£¨…ŤľĮļŌ![]() «ľĮļŌ
«ľĮļŌ![]() Ķń∑«Ņ’◊”ľĮ£¨
Ķń∑«Ņ’◊”ľĮ£¨![]() ÷–Ķń◊Óīů‘™ňōļÕ◊Ó–°‘™ňō÷ģ≤Ó≥∆ő™ľĮļŌ
÷–Ķń◊Óīů‘™ňōļÕ◊Ó–°‘™ňō÷ģ≤Ó≥∆ő™ľĮļŌ![]() Ķń÷Īĺ∂. ń«√īľĮļŌ
Ķń÷Īĺ∂. ń«√īľĮļŌ![]() ňý”–÷Īĺ∂ő™
ňý”–÷Īĺ∂ő™![]() Ķń◊”ľĮĶń‘™ňōłŲ ż÷ģļÕő™£® £©
Ķń◊”ľĮĶń‘™ňōłŲ ż÷ģļÕő™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() .
.
£®1£©»Ű![]() «Ķ•ĶųĶ›‘ŲļĮ ż£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣĽ
«Ķ•ĶųĶ›‘ŲļĮ ż£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣĽ
£®2£©»Ű![]() ļ„≥…ŃĘ£¨«ů Ķ żaĶń»°÷Ķ∑∂őß.
ļ„≥…ŃĘ£¨«ů Ķ żaĶń»°÷Ķ∑∂őß.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com