
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】某市数学教研室对全市2018级15000名的高中生的学业水平考试的数学成绩进行调研,随机选取了200名高中生的学业水平考试的数学成绩作为样本进行分析,将结果列成频率分布表如下:
数学成绩 | 频数 | 频率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合计 | 200 | 1 |
根据学业水平考试的数学成绩将成绩分为“优秀”、“合格”、“不合格”三个等级,其中成绩大于或等于80分的为“优秀”,成绩小于60分的为“不合格”,其余的成绩为“合格”.
(1)根据频率分布表中的数据,估计全市学业水平考试的数学成绩的众数、中位数(精确到0.1);
(2)市数学教研员从样本中又随机选取了![]() 名高中生的学业水平考试的数学成绩,如果这
名高中生的学业水平考试的数学成绩,如果这![]() 的最小值;
的最小值;
(3)估计全市2018级高中生学业水平考试“不合格”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系![]() 中,把到定点
中,把到定点![]() ,
,![]() 距离之积等于
距离之积等于![]() (
(![]() )的点的轨迹称为双纽线C.已知点
)的点的轨迹称为双纽线C.已知点![]() 是双纽线C上一点,下列说法中正确的有( )
是双纽线C上一点,下列说法中正确的有( )
①双纽线C关于原点O中心对称; ②![]() ;
;
③双纽线C上满足![]() 的点P有两个; ④
的点P有两个; ④![]() 的最大值为
的最大值为![]() .
.
A.①②B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,某十字路口的花圃中央有一个底面半径为
,某十字路口的花圃中央有一个底面半径为![]() 的圆柱形花柱,四周斑马线的内侧连线构成边长为
的圆柱形花柱,四周斑马线的内侧连线构成边长为![]() 的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器
的正方形.因工程需要,测量员将使用仪器沿斑马线的内侧进行测量,其中仪器![]() 的移动速度为
的移动速度为![]() ,仪器
,仪器![]() 的移动速度为
的移动速度为![]() .若仪器
.若仪器![]() 与仪器
与仪器![]() 的对视光线被花柱阻挡,则称仪器
的对视光线被花柱阻挡,则称仪器![]() 在仪器
在仪器![]() 的“盲区”中.
的“盲区”中.



(1)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 在点
在点![]() 处,仪器
处,仪器![]() 在
在![]() 上距离点
上距离点![]()
![]() 处,试判断仪器
处,试判断仪器![]() 是否在仪器
是否在仪器![]() 的“盲区”中,并说明理由;
的“盲区”中,并说明理由;
(2)如图![]() ,斑马线的内侧连线构成正方形
,斑马线的内侧连线构成正方形![]() ,仪器
,仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,同时仪器
移动,同时仪器![]() 从点
从点![]() 出发向点
出发向点![]() 移动,在这个移动过程中,仪器
移动,在这个移动过程中,仪器![]() 在仪器
在仪器![]() 的“盲区”中的时长为多少?
的“盲区”中的时长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,直线
轴非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为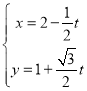 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)在(1)中,设曲线![]() 经过伸缩变换
经过伸缩变换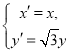 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任意一点为
上任意一点为![]() ,当点
,当点![]() 到直线
到直线![]() 的距离取最大值时,求此时点
的距离取最大值时,求此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: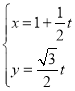 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com