
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)已知函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】产能利用率是工业总产出对生产设备的比率,反映了实际生产能力到底有多少在运转发挥生产作用.汽车制造业的产能利用率的正常值区间为![]() ,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
,称为“安全线”.如图是2017年第3季度到2019年第4季度的中国汽车制造业的产能利用率的统计图.以下结论正确的是( )
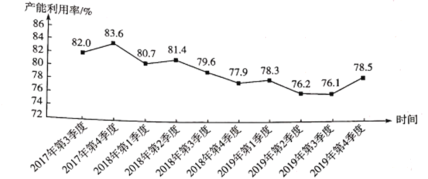
A.10个季度中,汽车产能利用率低于“安全线”的季度有5个
B.10个季度中,汽车产能利用率的中位数为![]()
C.2018年4个季度的汽车产能利用率的平均数为![]()
D.与上一季度相比,汽车产能利用率变化最大的是2019年第4季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为( )(参考数据![]() )
)
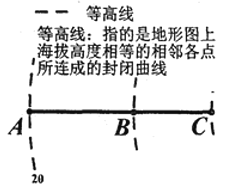
A.30米B.50米C.60米D.70米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF![]() a,以下结论正确的有( )
a,以下结论正确的有( )

A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的![]()
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某种药品的主要药理成分在国家药品监督管理局规定的值范围内,某制药厂在该药品的生产过程中,检验员在一天中按照规定每间隔2小时对该药品进行检测,每天检测4次:每次检测由检验员从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:![]() )根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布
)根据生产经验,可以认为这条药品生产线正常状态下生产的产品的其主要药理成分含量服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示某次抽取的20件产品中其主要药理成分含量在
表示某次抽取的20件产品中其主要药理成分含量在![]() 之外的药品件数,求
之外的药品件数,求![]() 的数学期望;
的数学期望;
(2)在一天的四次检测中,如果有一次出现了主要药理成分含量在![]() 之外的药品,就认为这条生产线在这一天的生产过程可能出现异常情况,需对本次的生产过程进行检查;如果有两次或两次以上出现了主要药理成分含量在
之外的药品,就认为这条生产线在这一天的生产过程可能出现异常情况,需对本次的生产过程进行检查;如果有两次或两次以上出现了主要药理成分含量在![]() 之外的药品,则需停止生产并对原材料进行检测.
之外的药品,则需停止生产并对原材料进行检测.
①下面是检验员在某次抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得,![]() ,
, .其中
.其中![]() 为抽取的第
为抽取的第![]() 件药品的主要药理成分含量
件药品的主要药理成分含量![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
②试确定一天中需停止生产并对原材料进行检测的概率(精确到0.001).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com