练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    2013年6月“神舟”发射成功．这次发射过程共有四个值得关注的环节，即发射、实验、授课、返回．据统计，由于时间关系，某班每位同学收看这四个环节的直播的概率分别为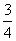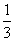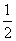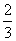，，，，并且各个环节的直播收看互不影响．

    (1)现有该班甲、乙、丙三名同学，求这3名同学至少有2名同学收看发射直播的概率；

    (2)若用X表示该班某一位同学收看的环节数，求X的分布列．


    解　(1)设“这3名同学至少有2名同学收看发射直播”为事件A，

    ＝；

    P(X＝4)＝×××＝.

    即X的分布列

    X

    0

    1

    2

    3

    4

    P

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某班级要从4名男生、2名女生中选派4人参加社区服务，如果要求至少有1名女生，那么不同的选派方案种数为________．(用数字作答)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设连续掷两次骰子得到的点数分别为m，n，令平面向量a＝(m，n)，b＝(1，－3)．

    (1)求使得事件“a⊥b”发生的概率；

    (2)求使得事件“|a|≤|b|”发生的概率；

    (3)求使得事件“直线y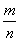＝x与圆(x－3)2＋y2＝1相交”发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


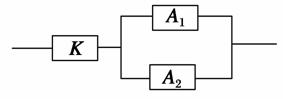
    如图，用K，A1，A2三类不同的元件连接成一个系统．当K正常工作且A1，A2至少有一个正常工作时，系统正常工作．已知K，A1，A2正常工作的概率依次为0.9、0.8、0.8，则系统正常工作的概率为(　　)

    A．0.960                                B．0.864

    C．0.720                                D．0.576

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设随机变量X～N(3,1)，若P(X>4)＝p，则P(2<X<4)＝(　　)

    A.＋p                                 B．1－p

    C．1－2p                                D.－p

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    袋中有20个大小相同的球，其中记上0号的有10个，记上n号的有n个(n＝1,2,3,4)，现从袋中任取一球，ξ表示所取球的标号．

    (1)求ξ的分布列、期望和方差；

    (2)若η＝aξ＋b，E(η)＝1，D(η)＝11，试求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图1­2所示，则该几何体的表面积为(　　)

    图1­2

    A．54  B．60  C．66  D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图1­4所示，在四棱锥P ­ ABCD中，PA⊥底面ABCD,  AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．

    (1)证明：BE⊥DC；

    (2)求直线BE与平面PBD所成角的正弦值；

    (3)若F为棱PC上一点，满足BF⊥AC，求二面角F ­ AB ­ P的余弦值．

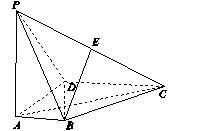
    图1­4

    查看答案和解析>>

    同步练习册答案