星级口算天天练系列答案科目：高中数学 来源： 题型：
某市在每年的春节后，市政府都会发动公务员参与到植树活动中去，林管部门在植树前，为保证树苗的质量，都会对树苗进行检测，现从甲、乙两种树苗中各抽测了10株树苗的高度，量出的高度如下(单位：厘米)：
甲：37,21,31,20,29,19,32,23,25,33
乙：10,30,47,27,46,14,26,10,44,46
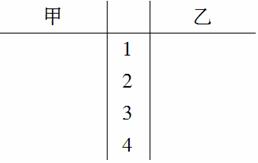
(1)根据抽测结果，完成下面的茎叶图(如图①所示)，并根据你填写的茎叶图，对甲、乙两种树苗的高度作比较，写出两个统计结论；
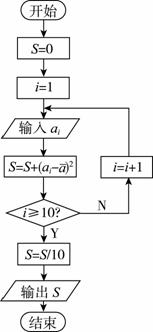
(2)设抽测的10株甲种树苗高度平均值为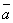
，将这10株树苗的高度依次输入按程序框图(如图②所示)进行运算，问输出的S大小为多少？并说明S的统计学意义．
②
查看答案和解析>>
科目：高中数学 来源： 题型：
一台机器由于使用时间较长，但还可以用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，下表为抽样试验结果.
| 转速x(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点 的零件数y(件) | 11 | 9 | 8 | 5 |
(1)画出散点图．
(2)如果y与x有线性相关关系，求线性回归方程．
(3)若实际生产中，允许每小时的产品中有缺点的零件最多为10件，那么机器的运转速度应控制在什么范围内？
查看答案和解析>>
科目：高中数学 来源： 题型：
有六名同学报名参加三个智力竞赛项目，在下列情况下各有多少种不同的报名方法？(不一定六名同学都能参加)
(1)每人恰好参加一项，每项人数不限；
(2)每项限报一人，且每人至多参加一项；
(3)每项限报一人，但每人参加的项目不限．
查看答案和解析>>
科目：高中数学 来源： 题型：
在第3、6、16路公共汽车的一个停靠站(假定这个车站只能停靠一辆公共汽车)，有一位乘客需在5分钟之内乘上公共汽车赶到厂里，他可乘3路或6路公共汽车到厂里，已知3路车和6路车在5分钟之内到此车站的概率分别为0.20和0.60，则该乘客在5分钟内能乘上所需要的车的概率为( )
A．0.20 B．0.60
C．0.80 D．0.12
查看答案和解析>>
科目：高中数学 来源： 题型：
2013年6月“神舟”发射成功．这次发射过程共有四个值得关注的环节，即发射、实验、授课、返回．据统计，由于时间关系，某班每位同学收看这四个环节的直播的概率分别为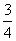
，
，
，
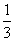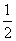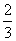，并且各个环节的直播收看互不影响．
(1)现有该班甲、乙、丙三名同学，求这3名同学至少有2名同学收看发射直播的概率；
(2)若用X表示该班某一位同学收看的环节数，求X的分布列．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的展开式的常数项是( )