
一台机器由于使用时间较长,但还可以用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表为抽样试验结果.
| 转速x(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点 的零件数y(件) | 11 | 9 | 8 | 5 |
(1)画出散点图.
(2)如果y与x有线性相关关系,求线性回归方程.
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10件,那么机器的运转速度应控制在什么范围内?
科目:高中数学 来源: 题型:
利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为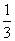 ,则在整个抽样过程中,每个个体被抽到的概率为( )
,则在整个抽样过程中,每个个体被抽到的概率为( )
A.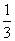 B.
B.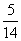
C.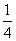 D.
D.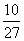
查看答案和解析>>
科目:高中数学 来源: 题型:
关于统计数据的分析,有以下5种说法:
①一组数不可能有两个众数;
②将一组数据中的每个数据都减去同一个数后,方差没有变化;
③调查影剧院中观众观看感受时,从50排(每排人数相同)中任意取一个排的人参加调查,属于分层抽样;
④一组数据的方差一定是正数;
⑤如图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在[50,60)的汽车大约是60辆.
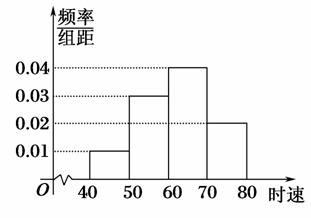
这5种说法中错误的是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
| 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
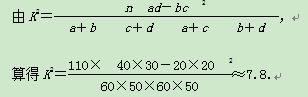 附表:
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
| 成绩 性别 | 不及格 | 及格 | 总计 |
| 男 | 6 | 14 | 20 |
| 女 | 10 | 22 | 32 |
| 总计 | 16 | 36 | 52 |
表2
| 视力 性别 | 好 | 差 | 总计 |
| 男 | 4 | 16 | 20 |
| 女 | 12 | 20 | 32 |
| 总计 | 16 | 36 | 52 |
表3
| 智商 性别 | 偏高 | 正常 | 总计 |
| 男 | 8 | 12 | 20 |
| 女 | 8 | 24 | 32 |
| 总计 | 16 | 36 | 52 |
表4
| 阅读量 性别 | 丰富 | 不丰富 | 总计 |
| 男 | 14 | 6 | 20 |
| 女 | 2 | 30 | 32 |
| 总计 | 16 | 36 | 52 |
A.成绩 B.视力
C.智商 D.阅读量
查看答案和解析>>
科目:高中数学 来源: 题型:
集合P={x,1},Q={y,1,2},其中x,y∈{1,2,3,…,9},且P⊆Q.把满足上述条件的一对有序整数对(x,y)作为一个点的坐标,则这样的点的个数是( )
A.9 B.14
C.15 D.21
查看答案和解析>>
科目:高中数学 来源: 题型:
设连续掷两次骰子得到的点数分别为m,n,令平面向量a=(m,n),b=(1,-3).
(1)求使得事件“a⊥b”发生的概率;
(2)求使得事件“|a|≤|b|”发生的概率;
(3)求使得事件“直线y=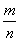 x与圆(x-3)2+y2=1相交”发生的概率.
x与圆(x-3)2+y2=1相交”发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com