练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

     

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

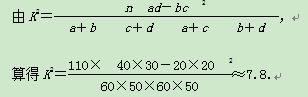    附表：

    P(K2≥k)

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是(　　)

    A．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

    B．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

    C．有99%以上的把握认为“爱好该项运动与性别有关”

    D．有99%以上的把握认为“爱好该项运动与性别无关”

     


    C

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在△ABC中，A为动点，B，C为定点，(a>0)，且满足条件sinC－sinB＝sinA，则动点A的轨迹方程是________．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某学校高一、高二、高三年级的学生人数之比是334，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取__________名学生．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知x是1,2,3，x,5,6,7这七个数据的中位数，且1,3，x，－y这四个数据的平均数为1，则＋y的最小值为__________．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从某校随机抽取100名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到数据分组及频数分布表和频率分布直方图.

    组号

    分组

    频数

    1

    [0,2)

    6

    2

    [2,4)

    8

    3

    [4,6)

    17

    4

    [6,8)

    22

    5

    [8,10)

    25

    续表

    6

    [10,12)

    12

    7

    [12,14)

    6

    8

    [14,16)

    2

    9

    [16,18)

    2

    合计

    100

    (1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；

    (2)求频率分布直方图中的a，b的值；

    (3)假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组．(只需写出结论)

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一台机器由于使用时间较长，但还可以用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，下表为抽样试验结果.

    转速x(rad/s)

    16

    14

    12

    8

    每小时生产有缺点

    的零件数y(件)

    11

    9

    8

    5

    (1)画出散点图．

    (2)如果y与x有线性相关关系，求线性回归方程．

    (3)若实际生产中，允许每小时的产品中有缺点的零件最多为10件，那么机器的运转速度应控制在什么范围内？

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据，结果统计如下：

    API

    [0,50]

    (50,100]

    (100,150]

    (150,200]

    (200,250]

    (250,300]

    >300

    空气

    质量

    优

    良

    轻微

    污染

    轻度

    污染

    中度

    污染

    中重度

    污染

    重度

    污染

    天数

    4

    13

    18

    30

    9

    11

    15

    　(1)若某企业每天由空气污染造成的经济损失S(单位：元)与空气质量指数API(记为w)的关系为：

    S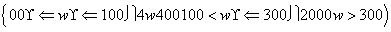＝试估计在本年度内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；

    (2)若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染．完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？

     

     

    非重度污染

    重度污染

    合计

    供暖季

    非供暖季

    合计

     

     

    100

    附：

    P(K2≥k0)

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

     

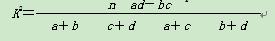
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有(　　)

    A．60种                                 B．70种

    C．75种                                 D．150种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{1,2}，B＝{1,2,3}，分别从集合A和B中随机取一个数a和b，确定平面上的一个点P(a，b)，记“点P(a，b)落在直线x＋y＝n上”为事件Cn(2≤n≤5，n∈N)，若事件Cn的概率最大，则n的所有可能值为(　　)

    A．3                                    B．4

    C．2和5                                D．3和4

    查看答案和解析>>

    同步练习册答案