
已知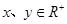 ,且
,且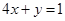 ,求
,求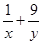 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为 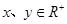 ,所以
,所以 ┄①,
┄①, ┄②,
┄②,
① ②得
②得 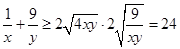 ,所以
,所以 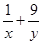 的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时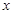 、
、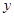 的值. .
的值. .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com