
若圆心在x轴上、半径为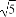 的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
(A)(x-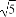 )2+y2=5 (B)(x+
)2+y2=5 (B)(x+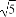 )2+y2=5
)2+y2=5
(C)(x-5)2+y2=5 (D)(x+5)2+y2=5
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十六第八章第七节练习卷(解析版) 题型:选择题
已知直线y=k(x+1)与抛物线C:y2=4x相交于A,B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
(A)±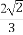 (B)±
(B)±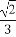
(C)± (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
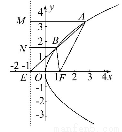
已知点M是直线3x+4y-2=0上的动点,点N为圆(x+1)2+(y+1)2=1上的动点,则|MN|的最小值是( )
(A) (B)1 (C)
(B)1 (C) (D)
(D)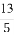
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十九第八章第十节练习卷(解析版) 题型:选择题
过抛物线y=2x2的焦点的直线与抛物线交于A(x1,y1),B(x2,y2),则x1x2=( )
(A)-2 (B)- (C)-4 (D)-
(C)-4 (D)-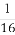
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:填空题
夹在两条平行线l1:3x-4y=0与l2:3x-4y-20=0之间的圆的最大面积为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:解答题
已知圆C与两圆x2+(y+4)2=1,x2+(y-2)2=1外切,圆C的圆心轨迹方程为L,设L上的点与点M(x,y)的距离的最小值为m,点F(0,1)与点M(x,y)的距离为n.
(1)求圆C的圆心轨迹L的方程.
(2)求满足条件m=n的点M的轨迹Q的方程.
(3)在(2)的条件下,试探究轨迹Q上是否存在点B(x1,y1),使得过点B的切线与两坐标轴围成的三角形的面积等于 .若存在,请求出点B的坐标;若不存在,请说明理由.
.若存在,请求出点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:选择题
已知点P在定圆O的圆内或圆周上,动圆C过点P与定圆O相切,则动圆C的圆心轨迹可能是( )
(A)圆或椭圆或双曲线
(B)两条射线或圆或抛物线
(C)两条射线或圆或椭圆
(D)椭圆或双曲线或抛物线
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
若直线l1:y=kx+k+2与l2:y=-2x+4的交点在第一象限,则实数k的取值范围是( )
(A)k>- (B)k<2 (C)-
(B)k<2 (C)- <k<2 (D)k<-
<k<2 (D)k<- 或k>2
或k>2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:选择题
已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2.给出以下结论:
①若e1与e2不共线,a与b共线,则k=-2;
②若e1与e2不共线,a与b共线,则k=2;
③存在实数k,使得a与b不共线,e1与e2共线;
④不存在实数k,使得a与b不共线,e1与e2共线.
其中正确结论的个数是( )
(A)1个(B)2个(C)3个(D)4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com