
已知非零向量e1,e2,a,b满足a=2e1-e2,b=ke1+e2.给出以下结论:
①若e1与e2不共线,a与b共线,则k=-2;
②若e1与e2不共线,a与b共线,则k=2;
③存在实数k,使得a与b不共线,e1与e2共线;
④不存在实数k,使得a与b不共线,e1与e2共线.
其中正确结论的个数是( )
(A)1个(B)2个(C)3个(D)4个
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:选择题
若圆心在x轴上、半径为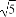 的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
(A)(x-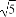 )2+y2=5 (B)(x+
)2+y2=5 (B)(x+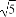 )2+y2=5
)2+y2=5
(C)(x-5)2+y2=5 (D)(x+5)2+y2=5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十第三章第四节练习卷(解析版) 题型:填空题
已知函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<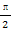 )的图象经过点(0,1),且
)的图象经过点(0,1),且 一个最高点的坐标为(1,2),则ω的最小值是 .
一个最高点的坐标为(1,2),则ω的最小值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:选择题
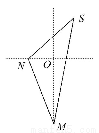
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与货轮相距20海里,随后货轮按北偏西30°的方向航行,30分钟后又测得灯塔在货轮的东北方向,则货轮航行的速度为( )
(A)20(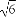 +
+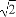 )海里/小时 (B)20(
)海里/小时 (B)20(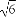 -
-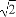 )海里/小时
)海里/小时
(C)20(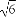 +
+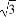 )海里/小时 (D)20(
)海里/小时 (D)20(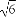 -
-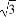 )海里/小时
)海里/小时
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:填空题
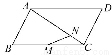
如图,在?ABCD中,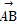 =a,
=a,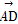 =b,
=b,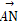 =3
=3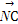 ,M是BC的中点,则
,M是BC的中点,则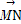 = (用a,b表示).
= (用a,b表示).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十六第四章第二节练习卷(解析版) 题型:选择题
已知向量a=(1,-2),b=(m,4),且a∥b,那么2a-b=( )
(A)(4,0)(B)(0,4)
(C)(4,-8)(D)(-4,8)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:填空题
若平面向量α,β满足|α|=1,|β|≤1,且以表示向量α,β的线段为邻边的平行四边形的面积为 ,则α与β的夹角θ的取值范围是 .
,则α与β的夹角θ的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十五第四章第一节练习卷(解析版) 题型:选择题
设A1,A2,A3,A4,A5是平面上给定的5个不同点,则使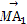 +
+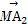 +
+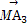 +
+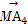 +
+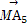 =0成立的点M的个数为( )
=0成立的点M的个数为( )
(A)0(B)1(C)5(D)10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十三第三章第七节练习卷(解析版) 题型:解答题
在△ABC中,A,B,C为三个内角,a,b,c为三条边, <C<
<C<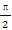 且
且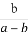 =
= .
.
(1)判断△ABC的形状.
(2)若| +
+ |=2,求
|=2,求 ·
· 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com