
【题目】函数f(x)=Asin(ωx+φ) ![]() 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)﹣cos2x,求函数g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.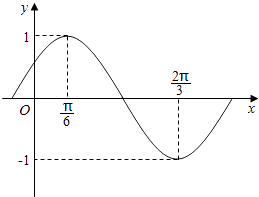
【答案】解:(Ⅰ)由图可得A=1, ![]() ,所以T=π.
,所以T=π.
所以ω=2.
当 ![]() 时,f(x)=1,可得
时,f(x)=1,可得 ![]() ,
,
因为 ![]() ,所以
,所以 ![]()
所以f(x)的解析式为 ![]() .
.
(Ⅱ) ![]()
= ![]()
= ![]() =
= ![]() .
.
因为 ![]() ,所以
,所以 ![]() .
.
当 ![]() ,即
,即 ![]() 时,g(x)有最大值,最大值为1;
时,g(x)有最大值,最大值为1;
当 ![]() ,即x=0时,g(x)有最小值,最小值为
,即x=0时,g(x)有最小值,最小值为 ![]()
【解析】(Ⅰ)由图可得A=1,一个周期内最高点与最低点的横坐标之差的绝对值为半个周期,得最小正周期T,进而得ω,代入最高点坐标求φ,得f(x)的解析式;(Ⅱ)由(Ⅰ)知f(x)的解析式,代入求出g(x)的解析式,用两角和的正弦公式把式中的第一项展开,合并,再逆用两角差的正弦公式把式子变形为一个角的一个三角函数值,由x的范围,得到2x﹣ ![]() 的范围,由正弦函数的图象得到sin(2x﹣
的范围,由正弦函数的图象得到sin(2x﹣ ![]() )的最大值和最小值.
)的最大值和最小值.
【考点精析】利用三角函数的最值对题目进行判断即可得到答案,需要熟知函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x<0时,f(x)=( ![]() )x .
)x .
(1)求当x>0时f(x)的解析式;
(2)画出函数f(x)在R上的图象; 
(3)写出它的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米. 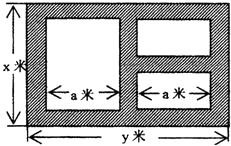
(1)分别写出用x表示y和S的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
B.“x=1”是“x2﹣3x+2=0”的充分必要条件.
C.命题p:“?x∈R,sinx+cosx≤ ![]() ”是真命题
”是真命题
D.若¬(p∧q)为真命题,则p、q至少有一个为假命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 与
与 ![]() 为互相垂直的单位向量,
为互相垂直的单位向量, ![]() ,
, ![]() 且
且 ![]() 与
与 ![]() 的夹角为锐角,则实数λ的取值范围是( )
的夹角为锐角,则实数λ的取值范围是( )
A.(﹣∞,﹣2) ![]()
B.( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
) ![]()
D.(﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为![]() 的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
的半圆形铁皮上截取一块矩形材料ABCD(点A、B在直径上,点C、D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗),
(1)若要求圆柱体罐子的侧面积最大,应如何截取?
(2)若要求圆柱体罐子的体积最大,应如何截取?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
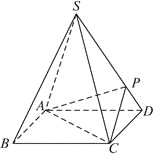
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com