
°Њћвƒњ°њƒ≥µЎЈљ’юЄЃ„Љ±Є‘Џ“їњй√жїэ„гєїіуµƒїƒµЎ…ѕљ®“ї»зЌЉЋщ Њµƒ“їЄцЊЎ–ќ„џЇѕ–‘–Ёѕ–єг≥°£ђ∆д„№√жїэќ™3000∆љЈљ√„£ђ∆д÷–≥°µЎЋƒ÷№£®“х”∞≤њЈ÷£©ќ™Ќ®µј£ђЌ®µјњнґ»Њщќ™2√„£ђ÷–Љдµƒ»эЄцЊЎ–ќ«ш”тљЂ∆ћ…иЋ№љЇµЎ√ж„чќ™‘Ћґѓ≥°µЎ£®∆д÷–ЅљЄц–°≥°µЎ–ќ„іѕаЌђ£©£ђЋ№љЇ‘Ћґѓ≥°µЎ’ЉµЎ√жїэќ™S∆љЈљ√„£Ѓ 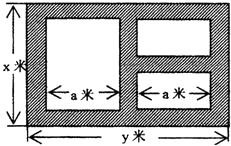
£®1£©Ј÷±р–і≥ц”√x±н ЊyЇЌSµƒЇѓ эєЎѕµ љ£®–і≥цЇѓ эґ®“е”т£©£ї
£®2£©‘х—щ…иЉ∆ƒ№ єS»°µ√„оіу÷µ£ђ„оіу÷µќ™ґа…ў£њ
°Њір∞Є°њ
£®1£©љв£Ї”…“—÷™xy=3000£ђ2a+6=y£ђ
‘тy= ![]() £ђ£®∆д÷–6°№x°№500£©£ї
£ђ£®∆д÷–6°№x°№500£©£ї
Ћщ“‘£ђ‘Ћґѓ≥°’ЉµЎ√жїэќ™S=£®x©Б4£©a+£®x©Б6£©a=£®2x©Б10£©a
=£®2x©Б10£© ![]() =£®x©Б5£©£®y©Б6£©
=£®x©Б5£©£®y©Б6£©
=3030©Б6x©Б ![]() £ђ£®∆д÷–6°№x°№500£©
£ђ£®∆д÷–6°№x°№500£©
£®2£©љв£Ї’ЉµЎ√жїэS=3030©Б6x©Б ![]() =3030©Б£®6x+
=3030©Б£®6x+ ![]() £©°№3030©Б2
£©°№3030©Б2 ![]()
=3030©Б2°Ѕ300=2430£ї
µ±«“љцµ±6x= ![]() £ђЉіx=50 ±£ђ°∞=°±≥…ЅҐ£ђіЋ ±x=50£ђy=60£ђSmax=2430£Ѓ
£ђЉіx=50 ±£ђ°∞=°±≥…ЅҐ£ђіЋ ±x=50£ђy=60£ђSmax=2430£Ѓ
Љі…иЉ∆x=50√„£ђy=60√„ ±£ђ‘Ћґѓ≥°µЎ√жїэ„оіу£ђ„оіу÷µќ™2430∆љЈљ√„
°Њљвќц°њ£®1£©„№√жїэќ™xy=3000£ђ«“2a+6=y£ђ‘тy= ![]() £ђ£®∆д÷–6°№x°№500£©£їЋщ“‘£ђ‘Ћґѓ≥°’ЉµЎ√жїэќ™S=£®x©Б4£©a+£®x©Б6£©a£ђ’ыјнЉіµ√£ї£®2£©”…£®1£©÷™£ђ’ЉµЎ√жїэS=3030©Б6x©Б
£ђ£®∆д÷–6°№x°№500£©£їЋщ“‘£ђ‘Ћґѓ≥°’ЉµЎ√жїэќ™S=£®x©Б4£©a+£®x©Б6£©a£ђ’ыјнЉіµ√£ї£®2£©”…£®1£©÷™£ђ’ЉµЎ√жїэS=3030©Б6x©Б ![]() =3030©Б£®6x+
=3030©Б£®6x+ ![]() £©£ђ”…їщ±Њ≤їµ» љњ…µ√Їѓ эµƒ„оіу÷µ£ђ“‘Љ∞ґ‘”¶µƒxµƒ÷µ£Ѓ
£©£ђ”…їщ±Њ≤їµ» љњ…µ√Їѓ эµƒ„оіу÷µ£ђ“‘Љ∞ґ‘”¶µƒxµƒ÷µ£Ѓ



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ эf£®x£©=loga£®x+1£©£ђg£®x£©=loga£®1©Бx£©∆д÷–£®a£Њ0«“a°ў1£©£Ѓ
£®1£©≈–ґѕf£®x£©©Бg£®x£©µƒ∆ж≈Љ–‘£ђ≤ҐЋµ√чјн”…£ї
£®2£©«у єf£®x£©©Бg£®x£©£Њ0≥…ЅҐµƒxµƒЉѓЇѕ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™‘≤![]() Њ≠єэ
Њ≠єэ![]() °Ґ
°Ґ![]() £ђ‘≤–ƒ
£ђ‘≤–ƒ![]() ‘Џ÷±ѕя
‘Џ÷±ѕя![]() …ѕ£ђєэµг
…ѕ£ђєэµг![]() £ђ«“–±¬ ќ™
£ђ«“–±¬ ќ™![]() µƒ÷±ѕя
µƒ÷±ѕя![]() љї‘≤ѕаљї”Џ
љї‘≤ѕаљї”Џ![]() °Ґ
°Ґ![]() Ѕљµг£Ѓ
Ѕљµг£Ѓ
£®Ґс£©«у‘≤![]() µƒЈљ≥ћ£ї
µƒЈљ≥ћ£ї
£®Ґт£©£®i£©«лќ ![]() «Јсќ™ґ®÷µ£Ѓ»ф «£ђ«л«у≥цЄ√ґ®÷µ£ђ»ф≤ї «£ђ«лЋµ√чјн”…£ї
«Јсќ™ґ®÷µ£Ѓ»ф «£ђ«л«у≥цЄ√ґ®÷µ£ђ»ф≤ї «£ђ«лЋµ√чјн”…£ї
£®ii£©»ф![]() ќ™„ш±к‘≠µг£ђ«“
ќ™„ш±к‘≠µг£ђ«“![]() £ђ«у÷±ѕя
£ђ«у÷±ѕя![]() µƒЈљ≥ћ£Ѓ
µƒЈљ≥ћ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘ЏЋƒјвћ®![]() ÷–£ђµ„√ж
÷–£ђµ„√ж![]() ќ™∆љ––Ћƒ±я–ќ£ђ
ќ™∆љ––Ћƒ±я–ќ£ђ ![]() ќ™
ќ™![]() …ѕµƒµг.«“
…ѕµƒµг.«“![]() .
.
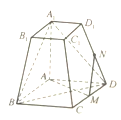
£®1£©«у÷§£Ї ![]() £ї
£ї
£®2£©»ф![]() ќ™
ќ™![]() µƒ÷–µг£ђ
µƒ÷–µг£ђ ![]() ќ™јв
ќ™јв![]() …ѕµƒµг£ђ«“
…ѕµƒµг£ђ«“![]() ”л∆љ√ж
”л∆љ√ж![]() Ћщ≥…љ«µƒ’эѕ“÷µќ™
Ћщ≥…љ«µƒ’эѕ“÷µќ™![]() £ђ ‘«у
£ђ ‘«у![]() µƒ≥§.
µƒ≥§.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ÷±љ«„ш±кѕµ![]() ÷–£ђ«ъѕя
÷–£ђ«ъѕя![]() ”л
”л![]() ÷бЄЇ∞л÷бљї”Џµг
÷бЄЇ∞л÷бљї”Џµг![]() £ђ÷±ѕя
£ђ÷±ѕя![]() ”л
”л![]() ѕа«–”Џ
ѕа«–”Џ![]() £ђ
£ђ ![]() ќ™
ќ™![]() …ѕ»ќ“в“їµг£ђ
…ѕ»ќ“в“їµг£ђ ![]() ќ™
ќ™![]() ‘Џ
‘Џ![]() …ѕµƒ…д”∞£ђ
…ѕµƒ…д”∞£ђ ![]() ќ™
ќ™![]() µƒ÷–µг£Ѓ
µƒ÷–µг£Ѓ
£®Ґс£©«уґѓµг![]() µƒємЉ£
µƒємЉ£![]() µƒЈљ≥ћ£ї
µƒЈљ≥ћ£ї
£®Ґт£©ємЉ£![]() ”л
”л![]() ÷бљї”Џ
÷бљї”Џ![]() £ђµг
£ђµг![]() ќ™«ъѕя
ќ™«ъѕя![]() …ѕµƒµг£ђ«“
…ѕµƒµг£ђ«“![]() £ђ
£ђ ![]() £ђ ‘ћљЊњ»эљ«–ќ
£ђ ‘ћљЊњ»эљ«–ќ![]() µƒ√жїэ «Јсќ™ґ®÷µ£ђ»фќ™ґ®÷µ£ђ«у≥цЄ√÷µ£ї»фЈ«ґ®÷µ£ђ«у∆д»°÷µЈґќІ£Ѓ
µƒ√жїэ «Јсќ™ґ®÷µ£ђ»фќ™ґ®÷µ£ђ«у≥цЄ√÷µ£ї»фЈ«ґ®÷µ£ђ«у∆д»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™ ![]() £ђ
£ђ ![]() µƒЉ–љ«ќ™120°г£ђ|
µƒЉ–љ«ќ™120°г£ђ| ![]() |=2£ђ|
|=2£ђ| ![]() |=3£ђЉ«|
|=3£ђЉ«| ![]() =3
=3 ![]() ©Б2
©Б2 ![]() £ђ
£ђ ![]() =2
=2 ![]() +k
+k ![]() £Ѓ
£Ѓ
£®1£©»ф ![]() °Ќ
°Ќ ![]() £ђ«у µ эkµƒ÷µ£Ѓ
£ђ«у µ эkµƒ÷µ£Ѓ
£®2£© «Јсіж‘Џ µ эk£ђ єµ√ ![]() °ќ
°ќ ![]() £њЋµ√чјн”…£Ѓ
£њЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њє≤ѕнµ•≥µ»л„°»™÷Ё“ї÷№ƒк“‘јі£ђ“т∆д°∞¬ћ…Ђ≥ц––£ђµЌћЉїЈ±£°±µƒјнƒоґш±Є №»Ћ√«µƒѕ≤∞Ѓ£ђ÷µіЋ÷№ƒк÷ЃЉ £ђƒ≥їъєєќ™ЅЋЅЋљвє≤ѕнµ•≥µ є”√’яµƒƒкЅдґќ£ђ є”√∆µ¬ °Ґ¬ъ“вґ»µ»»эЄцЈљ√жµƒ–≈ѕҐ£ђ‘Џ»Ђ –ЈґќІƒЏЈҐЈ≈![]() ЈЁµч≤йќ Њн£ђїЎ ’µљ”––Іќ Њн
ЈЁµч≤йќ Њн£ђїЎ ’µљ”––Іќ Њн![]() ЈЁ£ђѕ÷і”÷–Ћжїъ≥й»°
ЈЁ£ђѕ÷і”÷–Ћжїъ≥й»°![]() ЈЁ£ђЈ÷±рґ‘ є”√’яµƒƒкЅдґќ°Ґ
ЈЁ£ђЈ÷±рґ‘ є”√’яµƒƒкЅдґќ°Ґ![]() ~
~![]() Ћк є”√’яµƒ є”√∆µ¬ °Ґ
Ћк є”√’яµƒ є”√∆µ¬ °Ґ![]() ~
~![]() Ћк є”√’яµƒ¬ъ“вґ»љш––їг„№£ђµ√µљ»зѕ¬»эЄц±нЄс£Ї
Ћк є”√’яµƒ¬ъ“вґ»љш––їг„№£ђµ√µљ»зѕ¬»эЄц±нЄс£Ї
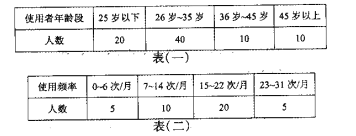
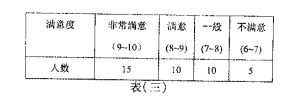
£®Ґс£©“јЊЁ…ѕ ц±нЄсЌк≥…ѕ¬Ѕ–»эЄцЌ≥Љ∆ЌЉ–ќ£Ї
£®Ґт£©ƒ≥≥««шѕ÷”–≥£„°»ЋњЏ![]() Ќт£ђ«л”√—щ±ЊєјЉ∆„№ћеµƒЋЉѕл£ђ ‘єјЉ∆ƒкЅд‘Џ
Ќт£ђ«л”√—щ±ЊєјЉ∆„№ћеµƒЋЉѕл£ђ ‘єјЉ∆ƒкЅд‘Џ![]() Ћк~
Ћк~![]() Ћк÷ЃЉд£ђ√њ‘¬ є”√є≤ѕнµ•≥µ‘Џ
Ћк÷ЃЉд£ђ√њ‘¬ є”√є≤ѕнµ•≥µ‘Џ![]() ~
~![]() іќµƒ»Ћ э.
іќµƒ»Ћ э.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њЇѓ эf£®x£©=Asin£®¶Ўx+¶’£© ![]() ≤њЈ÷ЌЉѕу»зЌЉЋщ Њ£Ѓ
≤њЈ÷ЌЉѕу»зЌЉЋщ Њ£Ѓ
£®Ґс£©«уf£®x£©µƒ„о–°’э÷№∆ЏЉ∞љвќц љ£ї
£®Ґт£©…иg£®x£©=f£®x£©©Бcos2x£ђ«уЇѓ эg£®x£©‘Џ«шЉд ![]() …ѕµƒ„оіу÷µЇЌ„о–°÷µ£Ѓ
…ѕµƒ„оіу÷µЇЌ„о–°÷µ£Ѓ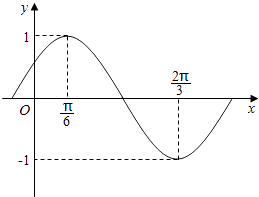
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™°—O£Їx2+y2=1ЇЌµгM£®4£ђ2£©£Ѓ
£®Ґс£©єэµгMѕт°—O“э«–ѕяl£ђ«у÷±ѕяlµƒЈљ≥ћ£ї
£®Ґт£©«у“‘µгMќ™‘≤–ƒ£ђ«“±ї÷±ѕяy=2x©Б1љЎµ√µƒѕ“≥§ќ™4µƒ°—MµƒЈљ≥ћ£ї
£®Ґу£©…иPќ™£®Ґт£©÷–°—M…ѕ»ќ“їµг£ђєэµгPѕт°—O“э«–ѕя£ђ«–µгќ™Q£Ѓ ‘ћљЊњ£Ї∆љ√жƒЏ «Јсіж‘Џ“їґ®µгR£ђ єµ√ ![]() ќ™ґ®÷µ£њ»фіж‘Џ£ђ«лЊў≥ц“їјэ£ђ≤Ґ÷Є≥цѕа”¶µƒґ®÷µ£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
ќ™ґ®÷µ£њ»фіж‘Џ£ђ«лЊў≥ц“їјэ£ђ≤Ґ÷Є≥цѕа”¶µƒґ®÷µ£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com