
【题目】下列命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
B.“x=1”是“x2﹣3x+2=0”的充分必要条件.
C.命题p:“?x∈R,sinx+cosx≤ ![]() ”是真命题
”是真命题
D.若¬(p∧q)为真命题,则p、q至少有一个为假命题.
【答案】B
【解析】解:根据原命题与逆否命题的定义即可知道A正确; 方程x2﹣3x+2=0的根为x=1,或2,
∴x=1能得到x2﹣3x+2=0,而x2﹣3x+2=0得不到x=1,
∴“x=1”是“x2﹣3x+2=0”的充分不必要条件,
即B是错误的;
“x∈R,sinx+cosx= ![]() sin(x+
sin(x+ ![]() )≤
)≤ ![]() ”,
”,
故命题p:“x∈R,sinx+cosx≤ ![]() ”是真命题,
”是真命题,
故C正确;
若¬(p∧q)为真命题,则p∧q是假命题,
则p,q至少1个是假命题;
故D正确,
故选:B.
【考点精析】通过灵活运用四种命题,掌握原命题:若P则q; 逆命题:若q则p;否命题:若┑P则┑q;逆否命题:若┑q则┑p即可以解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线为
的准线为![]() ,焦点为
,焦点为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求过点![]() ,且与
,且与![]() 相切的圆的方程;
相切的圆的方程;
(2)过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,
两点, ![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 的夹角为120°,|
的夹角为120°,| ![]() |=2,|
|=2,| ![]() |=3,记|
|=3,记| ![]() =3
=3 ![]() ﹣2
﹣2 ![]() ,
, ![]() =2
=2 ![]() +k
+k ![]() .
.
(1)若 ![]() ⊥
⊥ ![]() ,求实数k的值.
,求实数k的值.
(2)是否存在实数k,使得 ![]() ∥
∥ ![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车入住泉州一周年以来,因其“绿色出行,低碳环保”的理念而备受人们的喜爱,值此周年之际,某机构为了了解共享单车使用者的年龄段,使用频率、满意度等三个方面的信息,在全市范围内发放![]() 份调查问卷,回收到有效问卷
份调查问卷,回收到有效问卷![]() 份,现从中随机抽取
份,现从中随机抽取![]() 份,分别对使用者的年龄段、
份,分别对使用者的年龄段、![]() ~
~![]() 岁使用者的使用频率、
岁使用者的使用频率、![]() ~
~![]() 岁使用者的满意度进行汇总,得到如下三个表格:
岁使用者的满意度进行汇总,得到如下三个表格:
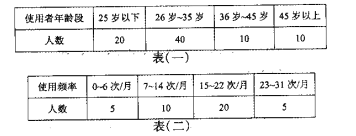
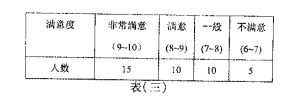
(Ⅰ)依据上述表格完成下列三个统计图形:
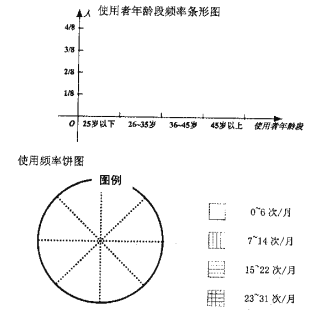
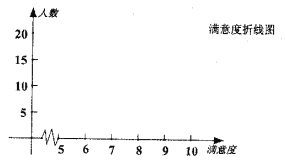
(Ⅱ)某城区现有常住人口![]() 万,请用样本估计总体的思想,试估计年龄在
万,请用样本估计总体的思想,试估计年龄在![]() 岁~
岁~![]() 岁之间,每月使用共享单车在
岁之间,每月使用共享单车在![]() ~
~![]() 次的人数.
次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ) ![]() 部分图象如图所示.
部分图象如图所示.
(Ⅰ)求f(x)的最小正周期及解析式;
(Ⅱ)设g(x)=f(x)﹣cos2x,求函数g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.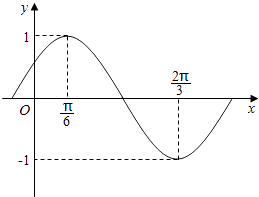
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的公差为d,前n项和为Sn , 等比数列{bn}的公比为q,已知b1=a1 , b2=2,q=d,S10=100.
(1)求数列{an},{bn}的通项公式
(2)当d>1时,记cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com