
【题目】每逢节日,电商之间的价格厮杀已经不是什么新鲜事,今年的6月18日也不例外.某电商在6月18日之后,随机抽取100名顾客进行回访,按顾客的年龄分成6组,得到如下频数分布表:
顾客年龄 |
|
|
|
|
|
|
频数 | 4 | 24 | 32 | 20 | 16 | 4 |
(1)在下表中作出这些数据的频率分布直方图;
(2)用分层抽样的方法从这100名顾客中抽取25人,再从抽取的25人中随机抽取2人,求年龄在![]() 内的顾客人数
内的顾客人数![]() 的分布列、数学期望.
的分布列、数学期望.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,四边形ABCD为直角梯形,
为正三角形,四边形ABCD为直角梯形,![]() //
//![]() ,平面
,平面![]() 平面ABCD,点E,F分别为AD,CP的中点,
平面ABCD,点E,F分别为AD,CP的中点,![]() .
.
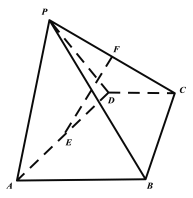
(1)证明:直线![]() //平面PAB;
//平面PAB;
(2)求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆心角为直角的扇形![]() 花草房,半径为1,点
花草房,半径为1,点![]() 是花草房弧上一个动点,不含端点,现打算在扇形
是花草房弧上一个动点,不含端点,现打算在扇形![]() 内种花,
内种花, ![]() ,垂足为
,垂足为![]() ,
, ![]() 将扇形
将扇形![]() 分成左右两部分,在
分成左右两部分,在![]() 左侧部分三角形
左侧部分三角形![]() 为观赏区,在
为观赏区,在![]() 右侧部分种草,已知种花的单位面积的造价为
右侧部分种草,已知种花的单位面积的造价为![]() ,种草的单位面积的造价为2
,种草的单位面积的造价为2![]() ,其中
,其中![]() 为正常数,设
为正常数,设![]() ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为
,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为![]()

求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
求当![]() 为何值时,总造价最小,并求出最小值。
为何值时,总造价最小,并求出最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某件产品的效率,随机抽查了100名工人某天生产该产品的数量,所取样本数据分组区间为![]() ,
,![]() 由此得到如图所示频率分布直方图.
由此得到如图所示频率分布直方图.
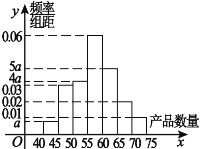
(1)求![]() 的值并估计该厂工人一天生产此产品数量的平均值;
的值并估计该厂工人一天生产此产品数量的平均值;
(2)从生产产品数量在![]() 的四组工人中,用分层抽样方法抽取13人,则每层各应抽取多少人?
的四组工人中,用分层抽样方法抽取13人,则每层各应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义[x]表示不超过x的最大整数,![]() ,例如:
,例如:![]() .执行如图所示的程序框图若输入的
.执行如图所示的程序框图若输入的![]() ,则输出结果为( )
,则输出结果为( )
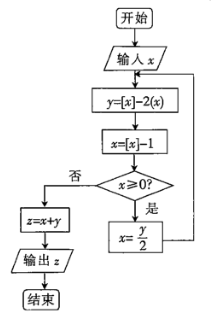
A.-4.6B.-2.8C.-1.4D.-2.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物是用户使用手机或电脑对所消费的商品或服务进行网络账务支付的一种服务方式,外卖、购物、买票等等我们生活的各个方面都可以通过网上来实现,某网络公司通过随机问卷调查,得到不同年龄段的网民在网上购物的情况.并从参与调查者中随机抽取了![]() 人.经统计得到如下表格:
人.经统计得到如下表格:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
在网上购物的人数 |
|
|
|
|
|
|
若把年龄大于或等于![]() 而小于
而小于![]() 岁的视为青少年,把年龄大于或等于
岁的视为青少年,把年龄大于或等于![]() 而小于
而小于![]() 岁的视为中年.把年龄大于或等于
岁的视为中年.把年龄大于或等于![]() 岁的视为老年,将频率视为概率.求:
岁的视为老年,将频率视为概率.求:
(1)在青少年,中年,老年中,哪个群休网上购物的概率最大?
(2)现从某市青少年网民(人数众多)中随机抽取![]() 人,设其中网上购物的人数为
人,设其中网上购物的人数为![]() .求随机变量
.求随机变量![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com