
| x |
| ex |
| (2-x)ex |
| e2 |
| x |
| ex |
| (x-2)ex |
| e2 |
| x |
| ex |
| (x-1)ex |
| x2 |
| 1 |
| e |
| x |
| ex |
| (x-2)ex |
| e2 |
| (x-1)(e2x-e2) |
| ex+2 |
| (x-1)(-kx+1)ex |
| x2 |
| 1 |
| k |
| 1 |
| k |


科目:高中数学 来源: 题型:
. |
| a1a2a3a4a5 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
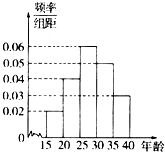 山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表:
山东省第二十三届运动会将于2014年9月16日在济宁市开幕,为办好省运会,济宁市计划招募各类志愿者1.2万人.为做好宣传工作,招募小组对济宁市15-40岁的人群随机抽取了100人,回答“省运会”的有关知识,根据统计结果制作了如下的统计图及表:| 组号 | 按年龄分组 | 回答完全正确人数 | 回答完全正确人数占本组频率 |
| 1 | [15,20) | 5 | 0.5 |
| 2 | [20,25) | a | 0.9 |
| 3 | [25,30) | 27 | x |
| 4 | [30,35) | 9 | 0.36 |
| 5 | [35,40) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
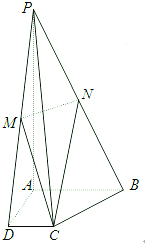 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
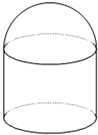 如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.查看答案和解析>>
科目:高中数学 来源: 题型:
| 寿命(天) | 频数 | 频率 |
| [100,200) | 10 | 0.05 |
| [200,300) | 30 | a |
| [300,400) | 70 | 0.35 |
| [400,500) | b | 0.15 |
| [500,600) | 60 | c |
| 合计 | 200 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com