练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．4名男歌手和2名女歌手联合举行一场音乐会，出场顺序要求两名女歌手之间恰有一名男歌手，共有出场方案的种数是192．

    分析 先从4名男歌手，选一名放在两名女歌手之间，并把他们捆绑在一起看做一个元素和另外的3名男歌手进行全排列，问题得以解决．

    解答 解：先从4名男歌手，选一名放在两名女歌手之间，并把他们捆绑在一起看做一个元素和另外的3名男歌手进行全排列，故有C41A22A44=192种不同的出场方案．
    故答案为：192．

    点评 本题排列组合的问题，相邻问题用捆绑，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

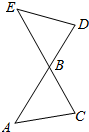    9．如图所示，某公园计划用鹅卵石铺成两条交叉的“健康石道”（线段AD和CE），并在这两条“健康石道”两端之间建设“花卉长廊”（线段AC和ED），以供市民休闲健身．已铺设好的部分BD=20m，ED=10$\sqrt{6}$m，∠BED=45°（△BDE为锐角三角形）．由于设计要求，未铺设好的部分AB和BC的总长只能为40m，则剩余的“花卉长廊”（线段AC）最短可以是20m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在下列函数中．值域不是[-$\sqrt{2}$，$\sqrt{2}$]的函数共有（　　）
    ①y=（sinx）′+（cosx）′②y=（sinx）′+cosx  ③y=sinx+（cosx）′④y=（sinx）′•（cosx）′．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

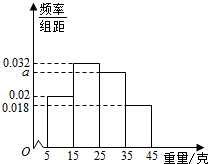    7．一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为（5，15]，（15，25]（25，35]，（35，45]，由此得到样本的重量频率分布直方图，如图．
    （Ⅰ）求a的值；
    （Ⅱ）根据样本数据，试估计盒子中小球重量的平均值；
    （Ⅲ）从盒子中随机抽取3个小球，其中重量在（5，15]内的小球个数为ξ，求ξ的分布列和数学期望及方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在平面直角坐标系xOy中，已知圆O：x2+y2=1，O1：（x-4）2+y2=4，动点P在直线x+$\sqrt{3}$y-b=0上，过P分别作圆O，O1的切线，且点分别为A，B，若满足PB=2PA的点P有且只有两个，则实数b的取值范围是-$\frac{20}{3}$＜b＜4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．求下列函数的导数
    （1）y=$\sqrt{{x}^{2}+1}$
    （2）y=sin22x
    （3）y=e-xsin2x
    （4）y=ln$\sqrt{1+{x}^{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求arctan$\frac{1}{3}$+arctan$\frac{1}{5}$+arctan$\frac{1}{7}$+arctan$\frac{1}{8}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在数列{an}中，a1=3，an=$\sqrt{{a}_{n-1}+2}$，则（　　）
    A．数列{an}单调递减B．数列{an}单调递增
    C．数列{an}先递减后递增D．数列{an}先递增后递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知m∈R，直线l：mx-（m+1）y=4m和圆C：x2+y2-8x+4y+16=0．
    （1）求直线l经过的定点坐标；
    （2）直线l能否将圆C分割成弧长的比值为$\frac{1}{2}$的两段圆弧？为什么？

    查看答案和解析>>

    同步练习册答案