
分析 求出P的轨迹方程,动点P在直线x+$\sqrt{3}$y-b=0上,满足PB=2PA的点P有且只有两个,转化为直线与圆x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,即可求出实数b的取值范围.
解答 解:由题意O(0,0),O1(4,0).设P(x,y),则
∵PB=2PA,
∴(x-4)2+y2=4(x2+y2),
∴x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0,
圆心坐标为(-$\frac{4}{3}$,0),半径为$\frac{8}{3}$,
∵动点P在直线x+$\sqrt{3}$y-b=0上,满足PB=2PA的点P有且只有两个,
∴直线与圆x2+y2+$\frac{8}{3}$x-$\frac{16}{3}$=0相交,
∴圆心到直线的距离d=$\frac{|-\frac{4}{3}-b|}{\sqrt{1+3}}$<$\frac{8}{3}$,
∴-$\frac{4}{3}$-$\frac{16}{3}$<b<-$\frac{4}{3}$+$\frac{16}{3}$
故答案为:-$\frac{20}{3}$<b<4.
点评 本题考查实数b的取值范围,考查轨迹方程,考查直线与圆的位置关系,正确转化是关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
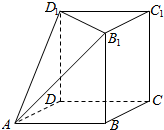 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
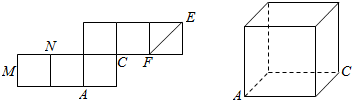 如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点
如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com