
分析 如图所示,由满足$\overline{AP}$+$\overline{BP}$=$λ(\overline{AM}+\overline{BM})$,其中λ∈R,|λ|>1,利用向量的平行四边形法则可得:O,M,P三点共线.设P(x1,y1),M(x2,y2),$\frac{{y}_{1}}{{x}_{1}}=\frac{{y}_{2}}{{x}_{2}}$=k≠0.分别利用点在双曲线与椭圆上可得$\frac{{x}_{1}^{2}-{a}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}}{{b}^{2}}$,$\frac{{x}_{2}^{2}-{a}^{2}}{{a}^{2}}$=-$\frac{{y}_{2}^{2}}{{b}^{2}}$.k1+k2=5,利用斜率计算公式可得5=$\frac{2{b}^{2}}{{a}^{2}}•\frac{1}{k}$.再利用向量计算公式即可得出k3+k4.
解答 解:如图所示,
∵满足$\overline{AP}$+$\overline{BP}$=$λ(\overline{AM}+\overline{BM})$,其中λ∈R,|λ|>1,
∴-2$\overrightarrow{PO}$=λ•(-2$\overrightarrow{MO}$),
∴O,M,P三点共线.
设P(x1,y1),M(x2,y2),$\frac{{y}_{1}}{{x}_{1}}=\frac{{y}_{2}}{{x}_{2}}$=k≠0.
则$\frac{{x}_{1}^{2}}{{a}^{2}}$-$\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{2}^{2}}{{a}^{2}}$+$\frac{{y}_{2}^{2}}{{b}^{2}}$=1,
∴$\frac{{x}_{1}^{2}-{a}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}}{{b}^{2}}$,$\frac{{x}_{2}^{2}-{a}^{2}}{{a}^{2}}$=-$\frac{{y}_{2}^{2}}{{b}^{2}}$,
∵k1+k2=5,
∴5=$\frac{{y}_{1}}{{x}_{1}+a}$+$\frac{{y}_{1}}{{x}_{1}-a}$=$\frac{2{x}_{1}{y}_{1}}{{x}_{1}^{2}-{a}^{2}}$=$\frac{2{x}_{1}{y}_{1}}{\frac{{{a}^{2}y}_{1}^{2}}{{b}^{2}}}$=$\frac{2{b}^{2}}{{a}^{2}}•\frac{1}{k}$.
∴k3+k4=$\frac{{y}_{2}}{{x}_{2}+a}+\frac{{y}_{2}}{{x}_{2}-a}$=$\frac{2{x}_{2}{y}_{2}}{{x}_{2}^{2}-{a}^{2}}$=-$\frac{2{b}^{2}}{{a}^{2}}$$•\frac{1}{k}$=-5.
故答案为:-5.
点评 本题考查了椭圆与双曲线的标准方程及其性质、向量的平行四边形法则、斜率计算公式,考查了推理能力与计算能力,属于难题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
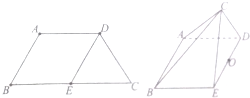 如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.
如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com